-ed Community, But Not Circles!
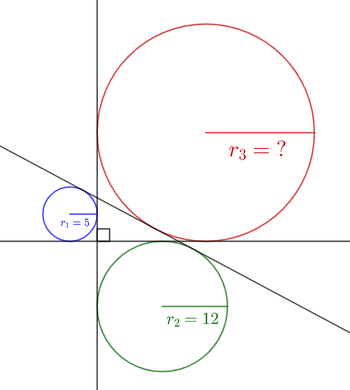
Given the right triangle and two excircles of radii and each adjacent to their respective legs, find the exradius of the third circle .
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The area of a triangle A = r s and A = s ( s − a ) ( s − b ) ( s − c ) , and in a right triangle, the inradius is r = 2 1 ( a + b − c ) = s − c .
The exradii have equations r a = s − a A , r b = s − b A , and r c = s − c A = r A = s .
By substitution, A = s ( s − a ) ( s − b ) ( s − c ) = s ⋅ r a A ⋅ r b A ⋅ r = r a r b A 3 , which solves to A = r a r b .
Substituting A = r a r b into r a = s − a A solves to r b = s − a , and similarly, r b = s − b A solves to r a = s − b .
Adding r b = s − a and r a = s − b gives r a + r b = 2 s − a − b = c , so c = r a + r b .
Substituting r = s − c into A = r s gives A = ( s − c ) s , which solves to s = 2 1 ( c + c 2 + 4 A ) .
And substituting A = r a r b and c = r a + r b into r c = s = 2 1 ( c + c 2 + 4 A ) gives r c = 2 1 ( r a + r b + ( r a + r b ) 2 + 4 r a r b ) .
Therefore, if r a = 5 and r b = 1 2 , then r c = 2 1 ( 5 + 1 2 + ( 5 + 1 2 ) 2 + 4 ⋅ 5 ⋅ 1 2 ) = 2 0 .