$x\lfloor x\rfloor$

Calculus Level 5

The function $f(x)=x\lfloor x \rfloor$ is tightly bounded by two parabolas.

For some positive integer $n$ , the area of the shape bounded by the function from $n-1$ to $n+1$ and these two parabolas is 2018.

Find the value of $n$

2018 2019 1010 1009

2 solutions

A Former Brilliant Member
Oct 27, 2018

$x^2-x \leq x\lfloor x\rfloor \leq x^2$

the area of the shape between $n-1$ and $n+1$ is

$\int_{n-1}^{n}(x^2)dx-\int_{n-1}^{n}\big((n-1)x\big)dx+\int_{n}^{n+1}(nx)dx-\int_{n}^{n+1}(x^2-x)dx=n$

So, $n=2018$

Thanks for sharing your solution. I didn't have time when I entered the problem last night and I was worried that no one had gotten it right. This is exactly how I did it. (Hopefully we are not the ones who are wrong.)

Jeremy Galvagni - 2 years, 7 months ago

the probability of us being wrong is 0.25 (at this very moment), in the worst case :) thanks for sharing the problem.

A Former Brilliant Member - 2 years, 7 months ago

Jeremy Galvagni
Oct 27, 2018

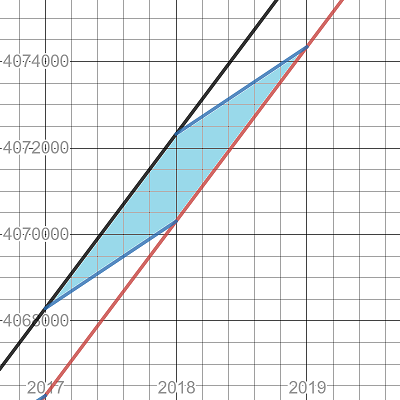
https://www.desmos.com/calculator/nv78n3ajhq

@Mehrdad Mohana has a great proof that for any $n$ the area is $n$ . I'll try to explain specifically why the answer is n=2018.

The blue segments are $f(x)$ from $2017$ to $2019$ , they are part of the lines $y=2017x$ and $y=2018x$ . The black and red curves are parts of $y=x^{2}$ and $y=x(x-1)$ respectively.

From 2017 to 2018 the area is $\int_{2017}^{2018}x^{2}dx - (2018\cdot 2017+2017^{2})/2=1008\frac{5}{6}$

From 2018 to 2019 the area is $(2019\cdot 2018+2018^{2})/2 - \int_{2018}^{2019}x(x-1)dx = 1009\frac{1}{6}$

Add these together and get 2018.

x ⌊ x ⌋ x\lfloor x\rfloor x ⌊ x ⌋

2 solutions

0 pending reports

$x\lfloor x\rfloor$