XY matters
⎩ ⎨ ⎧ x 2 − y 2 = 4 − 2 x y x + y = 2
If x and y satisfy the system of equations above, find the value of x − y .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
after substituting 2 to x+y, the equation should be x-y=x+y-xy not x-y=x+y+xy
wrong solution !
How do you get from the second line to the third line?
No! You can get y=0 x=2 from 2y=xy since if you regard x as 2, y can be every number.
x 2 − y 2 = 4 − 2 x y
x 2 + y 2 = 4 − 2 x y
→ 2 y 2 = 0 → y = 0 → x = 2 → x − y = 2
From the first equation we have that ( x + y ) ( x − y ) = 2 ( 2 − x y ) .
Then with x + y = 2 we see that x − y = 2 − x y , and so
( x + y ) − ( x − y ) = 2 − ( 2 − x y ) ⟹ 2 y = x y ⟹ y ( x − 2 ) = 0 .
So either y = 0 , which would in turn imply that x = 2 − y = 2 , or
x − 2 = 0 ⟹ x = 2 , which would in turn imply that y = 2 − x = 0 .
Either way we find that x = 2 , y = 0 , and so x − y = 2 − 0 = 2 .
Put y=2-x in the 1st eq. Which gives X^2- 4x+4=0 Then x=2 Y=0 and x-y=2 Hence solved.
x + y = 2 = > x 2 + y 2 + 2 x y = 4 summing both ecuations 4 + x 2 − y 2 = 4 − 2 x y + x 2 + y 2 + 2 x y = > y = 0 = > x + y = x − y
( x + y ) 2 = 4
⇔ x 2 − y 2 = ( x 2 + 2 x y + y 2 ) − 2 x y
⇔ x 2 − y 2 = x 2 + y 2
⇔ y = 0
⇔ x = 2
⇔ x − y = 2
x 2 − y 2 = 4 − 2 x y
SO: x 2 + 2 x y − y 2 = 4 (1)
x + y = 2
SO: ( x + y ) 2 = x 2 + 2 x y + y 2 = 4 (2)
equating (1) to (2): y 2 = − y 2
which is only true for y = 0
x + y = 2 SO x = 2
x 2 − y 2 = 4 − 2 x y . . . ( i )
x + y = 2 . . . ( i i )
Squaring both sides in ( i i ) ,
x 2 + 2 x y + y 2 = 4
Substituting in (i),
x 2 − y 2 = ( x 2 + 2 x y + y 2 ) − 2 x y
x 2 − y 2 = x 2 + y 2
y 2 = 0
y = 0
From ( i i ) , x = 2
x − y = 2 − 0 = 2
Hence, the answer is 2
x + y = 2 x 2 − y 2 = 4 − 2 x y ⇒ 2 x y = 4 + y 2 − x 2 ( x + y ) 2 = x 2 + 2 x y + y 2 ( x + y ) 2 = x 2 + ( 4 + y 2 − x 2 ) + y 2 ( x + y ) 2 = 2 y 2 + 4 4 = 2 y 2 + 4 ⇒ y = 0 x + y = 2 ⇒ x = 2 x − y = 2
Given: x 2 − y 2 = 4 − 2 x y ....[1]
x + y = 2 ...............................[2]
On equation [1], add 2 x y to both sides of the equation. You'll get:
x 2 + 2 x y − y 2 = 4 ...............[3]
Now square both sides of equation [2], and you'll get:
x 2 + 2 x y + y 2 = 4 ...............[4]
Subtract equation [3] from equation [4], the result will become:
2 y 2 = 0
y 2 = 0
y = 0 ......................................[5]
Substituting [5] into [2],
x + 0 = 2
x = 2
Now, since we got already the values of x and y , we can get the value of x − y .
Substituting the values we got for x and y , x − y = 2 − 0 = 2 .
Thus, the answer is 2 .
Moderator note:
Simple standard approach.
Given the system of equation: x 2 − y 2 = 4 − 2 x y ( E q n . 1 ) and x 2 + 2 x y + y 2 = 4 ( E q n . 2 ) Reduce the system makes up as: 2 x 2 + 2 x y = 8 − 2 x y Factor 2 both sides yields to: x 2 + x y = 4 − x y ⟹ x 2 + 2 x y = 4 Hence, let x 2 = 4 − 2 x y . So, x 2 − y 2 = x 2 . Reduce x 2 both sides yields to y 2 = 0 . Since x 2 = 4 , x − y = 2 . So, therefore, x 2 − y 2 = ( x − y ) ( x + y ) = 4 .
x^2-2xy+y^2=4<br> x^2+2xy-y^2=4<br> <br> 2x^2=8<br> <br> <br> x=2<br> <br> y=0<br>
my approach was............
W.K.T: x 2 − y 2 + 2 x i y = ( x + i y ) 2
applying it we get: ( x + i y ) 2 = 4 or x+iy=2 since there is no imaginary part y=0, x=2, x-y=2-0=2
Would you mind elaborating on your solution? I have no idea how you knew to use i , and I'm very curious to know if there is something I am missing here. And what is W.K.T.? Thanks.
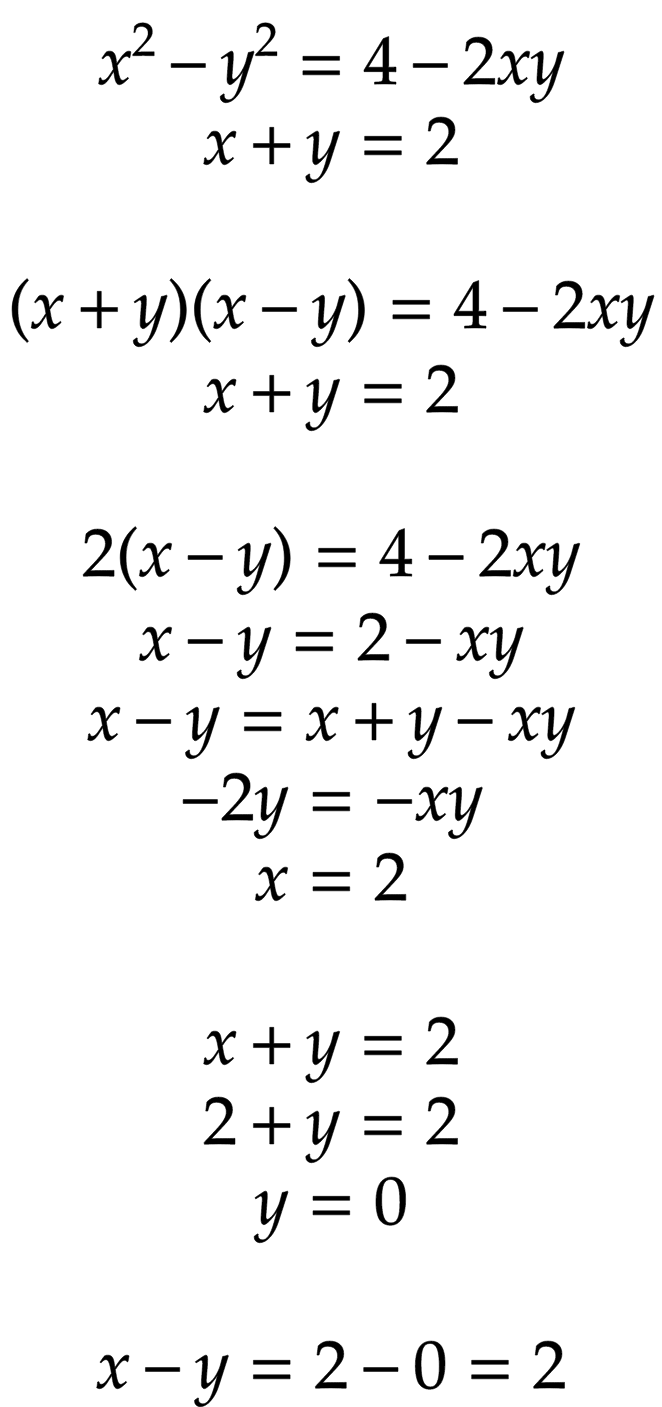

x 2 − y 2 = 4 − 2 x y
( x + y ) ( x − y ) = 2 ( 2 − x y )
2 ( x − y ) = 2 ( 2 − x y )
x − y = 2 − x y
subtitute 2 to x + y
x − y = x + y + x y
− 2 y = − x y
So, we get y = 0 x = 2
So, x − y = 2 .