Yahtzee Probability

Consider all the $6^5=7776$ ordered configurations after throwing all five dice. We classify them into 5 game states

Table 1. States and their initial probabilities. Note that all fractions can be expressed as 1296ths

Our strategy is as follows: once we have two or more dice of the same value, we start collecting that value, we put them aside and roll the rest.

When having a pair of a certain value (state B), we roll 3 dice, we have probability

• $\frac{125}{216}$ to throw none of that value; however this includes probability $\frac{5}{216}$ to throw a triplet with a new value (and we will decide to collect that new value, bringing us to state C) so $P(B|B)=\frac{120}{216}$
• $\frac{75}{216}$ (1/6 × 5/6 ×5/6 × 3) to roll one new die of that value, and in addition $\frac{5}{216}$ from the previous case, so $P(C|B)=\frac{80}{216}$
• $\frac{15}{216}$ 1/6 × 1/6 × 5/6 × 3 to roll two new dice of that value, so $P(D|B)=\frac{15}{216}$
• $\frac{1}{216}$ (1/6×1/6×1/6) to throw yahtzee, so $P(E|B)=\frac{1}{216}$

When having a triplet of a certain value (state C), we roll 2 dice, we have probability

• $\frac{25}{36}$ to throw none of that value so $P(C|C)=\frac{25}{36}$
• $\frac{10}{36}$ (1/6 × 5/6 × 2) to roll one new die of that value, so $P(D|C)=\frac{10}{36}$
• $\frac{1}{36}$ 1/6 × 1/6 to roll two new dice of that value, so $P(E|C)=\frac{1}{36}$

When having a quadruplet of a certain value (state D), we roll 1 die, we have probability

• $\frac{5}{6}$ not to throw that value so $P(D|D)=\frac{5}{6}$
• $\frac{1}{6}$ to throw it, so $P(E|D)=\frac{1}{6}$

Summarizing the state transition probabilities:

Table 2, state transition probabilities For example $P(D|C)=\frac{10}{36}$ is the probability to get from state C to state D in one roll. Note that the first row reflects the probabilities from table 1.

Next, we calculate the state probabilities after two rolls:

Table 3, state probabilities after two rolls

Finally, using tables 2 and 3, the probability to be in state E after 3 rolls is calculated as

$P_3(E)=P_2(A)P(E|A)+P_2(B)P(E|B) + ... =\frac{14400}{1679616}\frac{1}{1296}+\frac{756000}{1679616}\frac{1}{216}+...=\frac{100194336}{2176782336}=\frac{347897}{7558272}$ (about 4.6%).

The final answer then is $347897+7558272=\boxed{7,906,169}$

This is an example of the calculations I used. There are $6^5$ possible outcomes from the 1st roll. Say we have 3 matches. There are

$\begin{aligned} \binom{5}{3}\cdot6\cdot5\cdot5=1500 \end{aligned}$

ways this can happen; $\binom{5}{3}$ choices for which 3 match, 6 choices for the repeated number, and 5 choices for each of the other two numbers.

Let's say the matching number is $A$ . We roll two dice again. With probability $\frac{1}{36}$ , we roll $AA$ and get a Yahtzee straight away. With probability $\frac{10}{36}$ , we roll one $A$ and something else; we then have probability $\frac{1}{6}$ of getting the $A$ on the 3rd roll. With probability $\frac{25}{36}$ , we don't roll an $A$ on the 2nd roll, and have to roll $AA$ on the 3rd, with probability $\frac{1}{36}$ .

So overall, the probability of getting 3 matches after the 1st roll and going on to get a Yahtzee is

$\begin{aligned} \frac{1500}{6^5} \cdot \left( \frac{1}{36} + \frac{10}{36} \cdot \frac{1}{6} + \frac{25}{36} \cdot \frac{1}{36} \right) = \frac{1500}{6^7}+\frac{15000}{6^8}+\frac{37500}{6^9}=\frac{15125}{839808} \end{aligned}$

This gets tricky when we have only 1 or 2 matches after the 1st roll - as mentioned in the problem, the most common value can change in these cases. However, the same approach still works.

In summary, the probabilities are

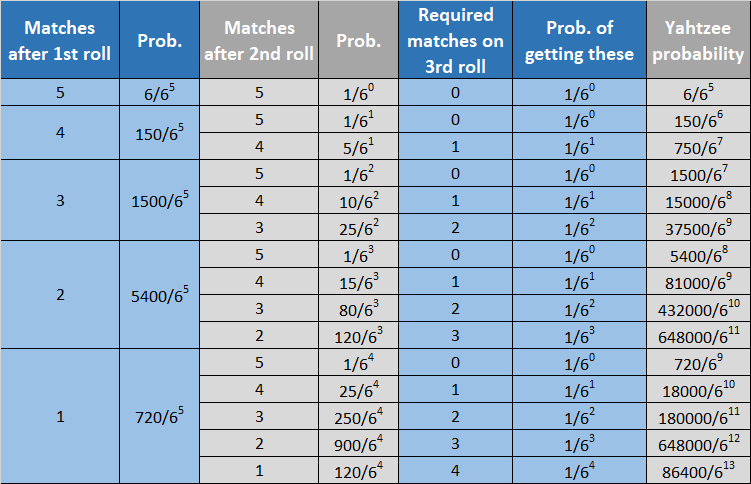
The total probability of a Yahtzee using this strategy is the sum of the final column, which comes out to be $\frac{347897}{7558272}$ , giving the final answer $347897+7558272=\boxed{7906169}$