Yay for 2014! #7

Area of the rectangle $=280$

Area of one red triangle $= \frac {1}{2} \times 14^2 \sin {60}=49 \sqrt {3}=A_1$

Area of the two white triangles $=2 \times \frac {100 \sqrt {3}}{3}= \frac {200 \sqrt {3}}{3}=A_2$

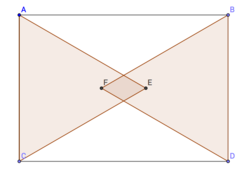Let the wanted area be $X$ ;

Then, $280-A_1-A_2=A_1-X$

Solving the equation we get $X= \frac {494 \sqrt {3}}{3}-280$

Hey, why can't I see this image?

Label points in the diagram as shown above. It is clear that the figure we are trying to find the area of, $FGEH$ , is a rhombus. Thus, if we let $[ABCD]$ be the area of $ABCD$ , we have

$[FGEH] = \frac{d_{1}d_{2}}{2} = \frac{(FE)(GH)}{2}.$

We have

$EF = AB - (IF + EJ) = AB - (IJ - FJ + IJ - IE) = 20 - (20 - 7\sqrt{3} + 20 - 7\sqrt{3}) = 14\sqrt{3} - 20$

and

$GH = 2GK = \frac{2FK}{\sqrt{3}} = \frac{FE}{\sqrt{3}} = \frac{14\sqrt{3} - 20}{\sqrt{3}} = \frac{42 - 20\sqrt{3}}{3}.$

Thus,

$[FGEH] = \frac{(FE)(GH)}{2} = \frac{(14\sqrt{3} - 20)(\frac{42 - 20\sqrt{3}}{3})}{2} = \frac{494\sqrt{3}}{3} - 280,$

and $a+b+c = \boxed{777}.$

We can find that $EF= 14 \sqrt{3} - 20$ .

We can split the rhombus into two triangles (the tip of the large equilateral triangles). We can see that the triangles are similar. The height of the small triangle is half of EF, or $\frac{14 \sqrt{3} - 20}{2} =7\sqrt{3}-10$ .

Using similar triangles, we can find the base to be $\frac{7 \sqrt{3}-10}{7 \sqrt{3}} \cdot 14=\frac{14\sqrt{3}-20}{\sqrt{3}}$ .

The area of the rhombus is twice the area of the triangle, or $2 \cdot \frac{1}{2} (7\sqrt{3}-10)(\frac{14\sqrt{3}-20}{\sqrt{3}})$ .

We simplify this to get $\frac{494-280\sqrt{3}}{\sqrt{3}}$ or $\frac{494\sqrt{3}}{3}-280$ .

Therefore, our final answer is $494+3+280=\boxed{777}$ .