Yay for 2014 in 2015
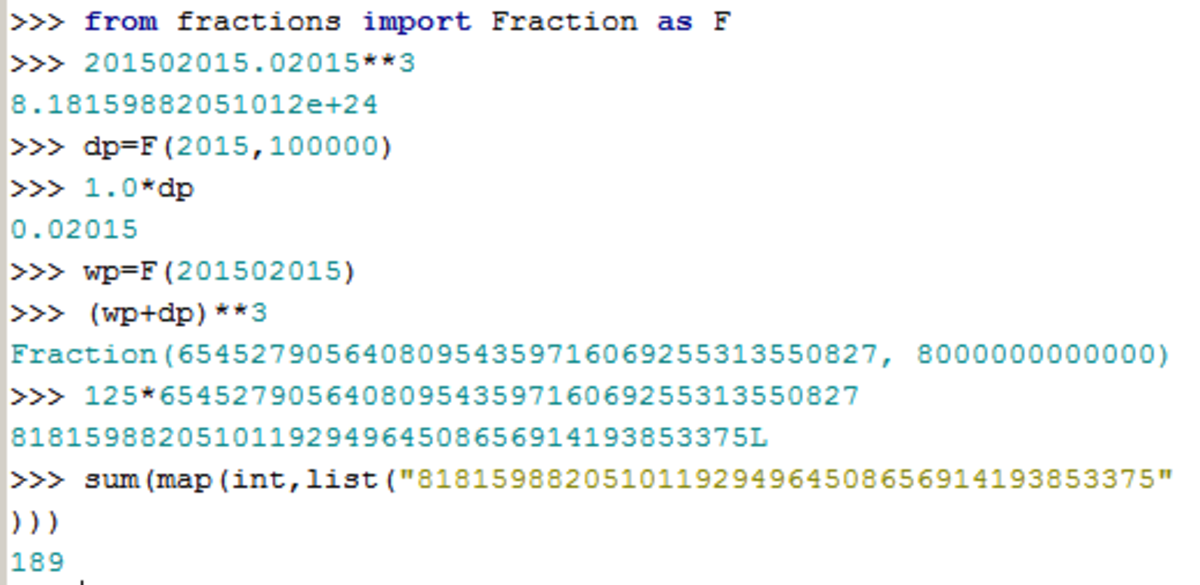
Given that , find the sum of the digits, including decimal places, of the exact value of .
(You may use a calculator to calculate the digit sum.)
Based on this problem I posted back in 2014.
The answer is 189.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Factor 2 0 1 5 3 out from our desired value. We have
( 2 0 1 5 0 2 0 1 5 . 0 2 0 1 5 ) 3 = 2 0 1 5 3 × ( 1 0 0 0 0 1 . 0 0 0 0 1 ) 3 = 2 0 1 5 3 × ( 1 0 5 + 1 + 1 0 − 5 ) 3 .
Expanding ( 1 0 5 + 1 + 1 0 − 5 ) 3 using ( a + b + c ) 3 = a 3 + b 3 + c 3 + 3 ( a 3 b + a b 2 + a 2 c + a c 2 + b 2 c + b c 2 ) + 6 a b c gives
( 1 0 0 0 0 1 . 0 0 0 0 1 ) 3 = 1 0 1 5 + 3 ( 1 0 1 0 ) + 6 ( 1 0 5 ) + 7 + 6 ( 1 0 − 5 ) + 3 ( 1 0 − 1 0 ) + 1 0 − 1 5 .
Finally, multiply 2 0 1 5 3 , which we know the value of, by these powers of 10. Careful arithmetic gives
( 2 0 1 5 0 2 0 1 5 . 0 2 0 1 5 ) 3 = 8 1 8 1 5 9 8 8 2 0 5 1 0 1 1 9 2 9 4 9 6 4 5 0 8 . 6 5 6 9 1 4 1 9 3 8 5 3 3 7 5 ,
which has digit sum 1 8 9 .