Yeah I know!

Calculus Level 4

lim ⁡ x → ∞ x 2 f ′ ′ ( x ) f ( x ) lim ⁡ t → 0 ( 1 + sin ⁡ t ) 1 − cos ⁡ t = n 3 − 5 n 2 + 2 n + 10 \large \lim_{x\to\infty} \dfrac{x^2 f''(x)}{f(x) } \lim_{t \to0}\ (1+\sin t)^{1 - \cos t} = n^3 - 5n^2 + 2n + 10

Let f f be a polynomial of degree n n satisfying the equation above. Given that f ′ ( x ) f'(x) has only one real root and f ( 1 ) = f ( − 1 ) f(1) = f(-1) .

If there exists a real k k satisfying f ′ ( k ) = 0 f'(k) = 0 , find ∫ 2 k + 1 k 2 − k + 1 f ( x ) d x \displaystyle \int_{2k+1}^{k^2-k+1} f(x) \, dx .


The answer is 0.

Abhi Kumbale by Abhi Kumbale , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Abhi Kumbale
May 25, 2016

1 Helpful 0 Interesting 0 Brilliant 0 Confused

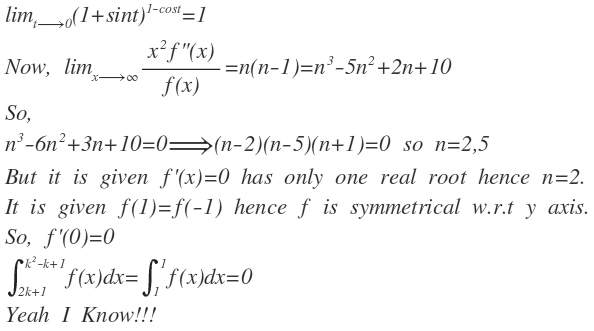
Can you explain why n=2 implies f'(x) has only one real root. Your explanation should be if n=5 then the condition of f(1)=f(-1) would not have been valid and as the leading term cannot be zero n is not equal to 5.

Arghyadeep Chatterjee - 3 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...