Yeah, you could be the greatest
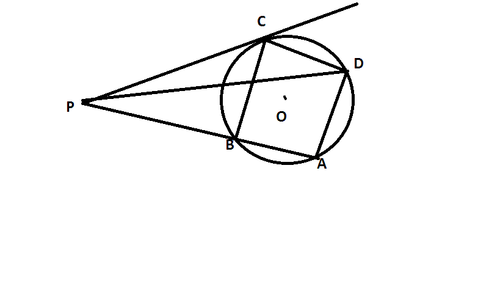 The square
is inscribed in a circle of radius 1 unit.
is a straight line,
is a tangent to the circle .The length of
is:
The square
is inscribed in a circle of radius 1 unit.
is a straight line,
is a tangent to the circle .The length of
is:
The answer is 3.162.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Because PC is tsngent, and angle BCD is 90 degrees, angle PCD is 135 degrees, and PCB is 45. Also, we can find the squares side lengths to be 2 . Because PC is tangent to the square, and PCD is 135 degrees, we know triangle BCP is a 45,45,90 with side lengths root 2. Using the Pythagoras theorem: 2 + 2 = 4 . The square of which is 2. So PC has a length of 2. We know two lengths and the angle, so we can use the law of cosines: a 2 = 2 2 + 2 2 − 2 ( 2 ) ( 2 ) ∗ c o s ( 1 3 5 ) . Solving for a, we get 1 0 .