Yellow area minus blue area
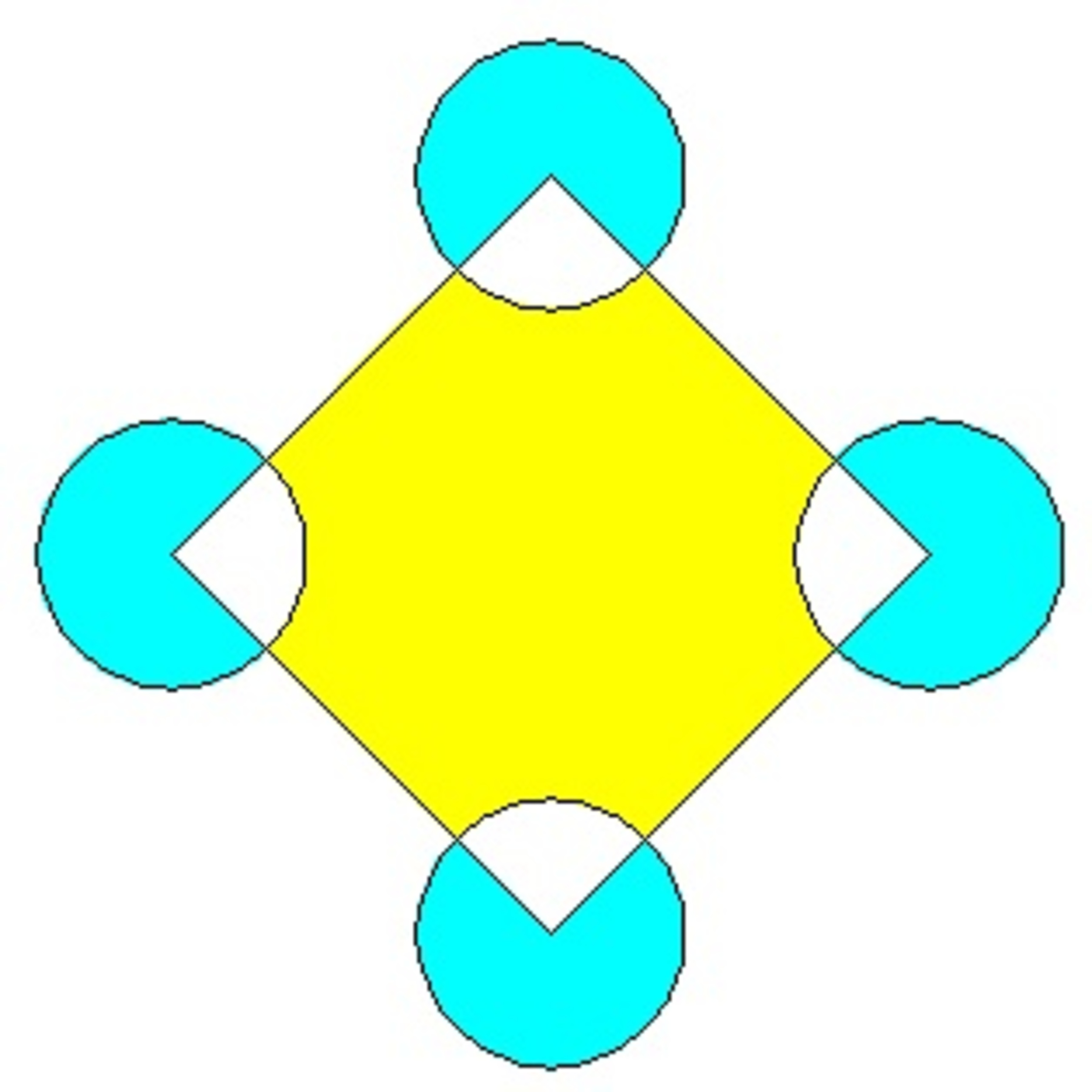 Four identical circles, each of radius
, are drawn at the vertices of a square of side length
. If
represents the area of the yellow region and
represents the area of the blue region, find
.
Four identical circles, each of radius
, are drawn at the vertices of a square of side length
. If
represents the area of the yellow region and
represents the area of the blue region, find
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The four quarter circles in the square area can be considered as a whole circle in the square. The area of one complete circle would be pi X (1^2) . Given that the side length of the square is 4, the area of the square is 4 X 4 and the area of the yellow region can be described as 4 X 4 - pi . The blue region are made up of four 4 3 circles, which, also, can be considered as three whole circles. Therefore, the area of the blue region is 3 X pi .
Thus, the area of y - b is 4 X 4 - pi - 3 X pi , which we can simplify and factorize into 4(4 - pi) .