Yellow Figure
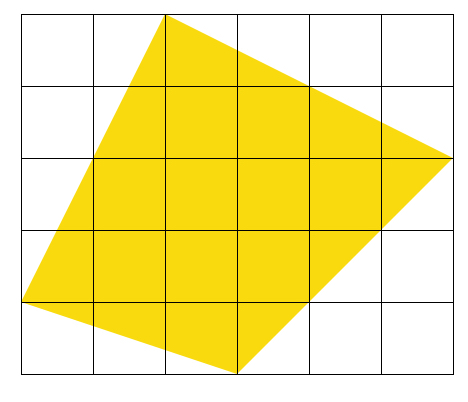
What is the area of the yellow figure?
Note: Each square has unit side length.
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
The formula of getting the area of a certain polygon given its vertices as lattice points in a coordinate plane expressed in Pick's Theorem is: A = I + B/2 – 1, where A here represents the area of that certain polygon, I the number of lattice points located inside the polygon, and B the number of lattice points located on the sides of the polygon. In this yellow figure, by counting the number of lattice points both located inside the polygon and on the boundary (on the sides of the polygon), we get: I = 13 and B = 8. Substituting I = 13 and B = 8 in Pick's formula A = I + B/2 – 1, we get A = 13 + 8/2 – 1 = 13 + 4 – 1 = 16. :)
http://artofproblemsolving.com/wiki/index.php?title=Pick%27s_Theorem
This can easily be done by subtracting the remaining area from the main square.The remaining areas are all 4 triangles whose total area is 14 so subtracting it from the square area i.e. 30 we will get our required answer i.e. 16......
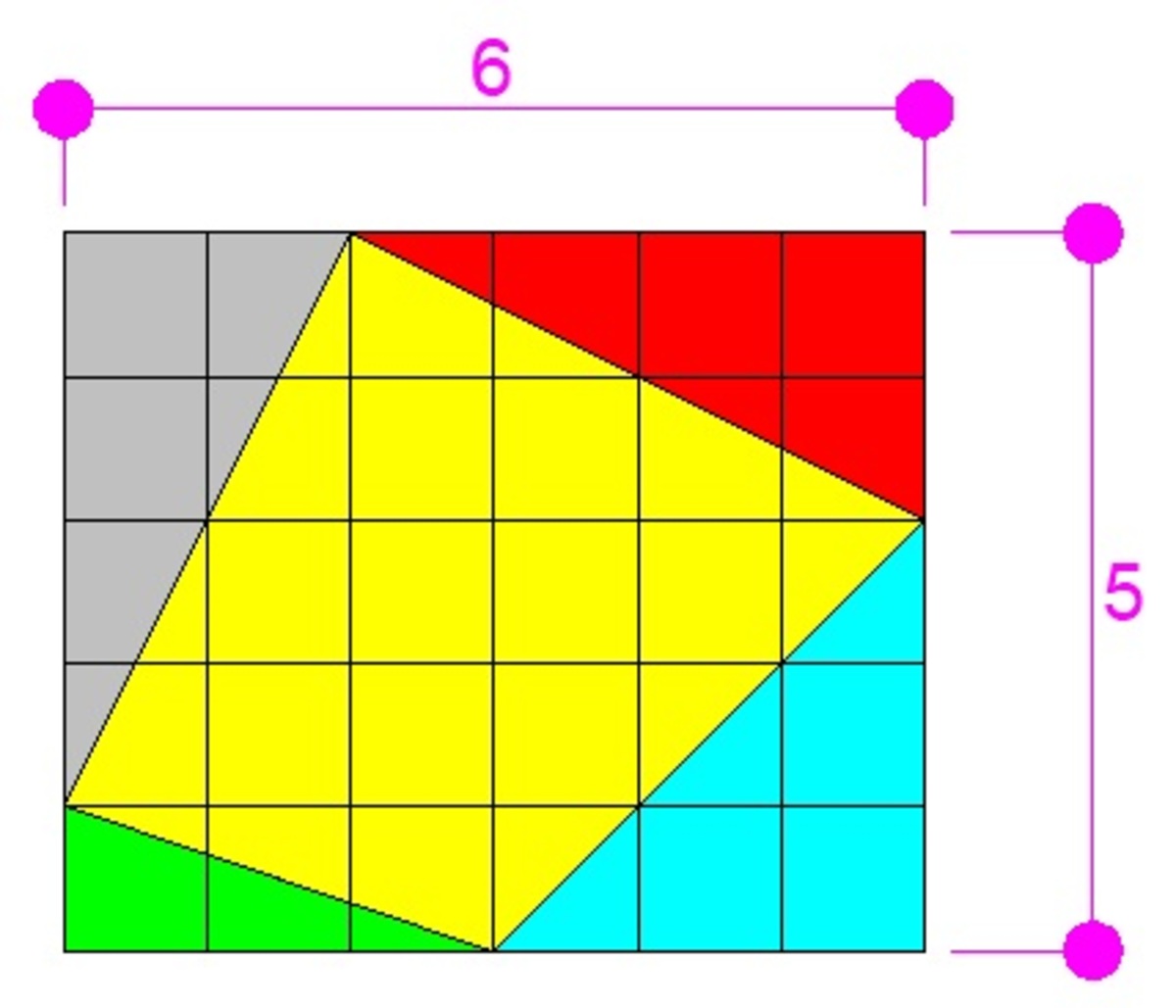 The area of the yellow region is equal to the area of the rectangle inscribing the yellow region minus the sum of the areas of the four triangles. We have
The area of the yellow region is equal to the area of the rectangle inscribing the yellow region minus the sum of the areas of the four triangles. We have
A = 6 ( 5 ) − 2 1 [ 2 ( 4 ) + 1 ( 3 ) + 3 ( 3 ) + 2 ( 4 ) ] = 1 6
Count all the squares, all full squares are square unit and all partial squares have another partial somewhere to complete it. 9 full squares and 14 partials, 9 + 14÷2 = 16. I believe this only works for vertex of polygons on integer coordinates
Let's break this figure into 5 rectangles as shown below.
The area of the yellow region in the 1st rectangle is exactly half the area of the 4 × 2 rectangle, so the area is 4 × 2 ÷ 2 = 4 .
Similarly, the area of the yellow region in the 3rd rectangle is exactly half the area of the 2 × 4 rectangle, so the area is 2 × 4 ÷ 2 = 4 .
We can work out the areas of the yellow region in the 4th and 5th rectangle to 2 3 and 2 9 .
And the area of the yellow region in the 3rd rectangle is just 2 × 1 = 2 .
So the total area of the yellow region is the sum of these areas, 4 + 4 + 2 3 + 2 9 + 2 = 1 6 .
Bonus : Anyone wants to solve this question using Pick's theorem ?