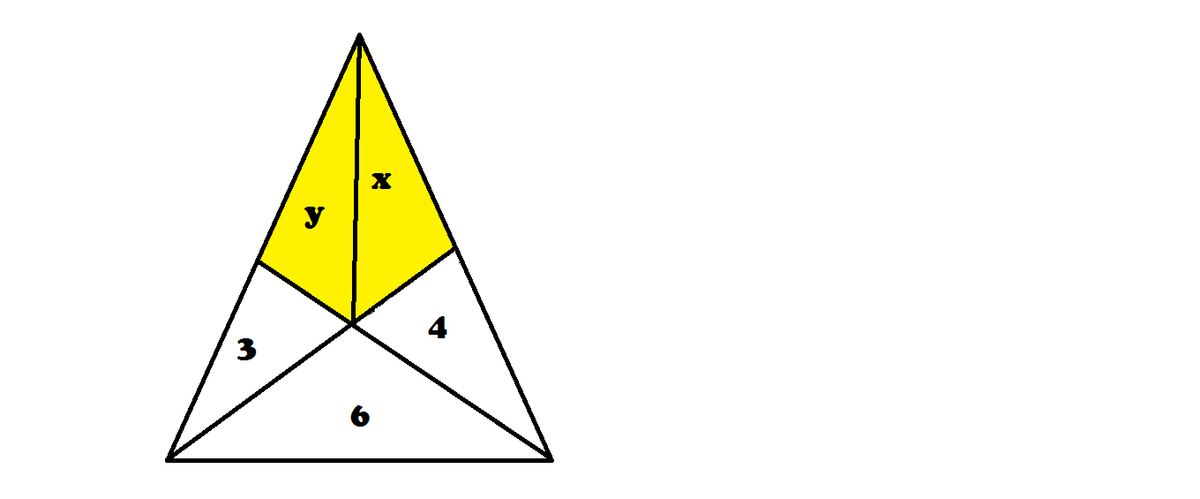
Yellow Quadrilateral
The numbers 3 , 4 , and 6 denote the areas enclosed by their respective triangles.
What is the area of the yellow region?
The answer is 9.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
hey, may be, m wrong. but your solution is not exactly seem like as menelaus theorem, and according to me you just solve it by taking the angle DOB and DOE 90deg (how does it come?) , so that OD will be the height of adjacent triangles, and Area BOD/ area EOD= [0.5* BO* OD/ 0.5* EO* OD]
and then BOD/EOD= BO/EO
Log in to reply
No; whatever the angles ∠ D O B , ∠ D O E are, as long as E , O , B are collinear, the ratio of areas [ D O E ] [ D O B ] is equal to the ratio of their respective base lengths O E O B . Just observe that they have the same altitude (this altitude is not necessarily D O ).
A nice, elegant solution. Moreover, this leads to an interesting theorem I wish I'd discovered sooner: If a quadrilateral is split into triangles by its diagonals, and their areas are a , b , c and d going around, then a c = b d .
Log in to reply
This is easy to show. WLOG, let $a,c$ and $b,d$ be opposing corner triangles in the quadrilateral. Then, by looking at either diagonal, let's say it's the one that splits quadrilateral into two triangles $a,b$ and $c,d$. By ratio of areas of triangles with same height is ratio of their bases, we see that $a/b = d/c$.
Isn't the ratio of the bases/ or height the root of the ratio of their areas? answer will still be the same though
Log in to reply
That's in the case of similarity....here we are just talking two triangles having same altitude
Exactly what is wrong with the following fallacious argument? Denote the large triangle by ABC, with A at the top, B at lower left, and C at lower right. Let D be the point between A and B, and E the point between A and C. Let O be the intersection of DC and EB. The area of a triangle is given by (1/2)RT*sin(included angle). For convenience, let a =DO, b = EO, x = BO, and y = CO. Letting Y = the area of the yellow triangle, we apply the general formula to each of the four triangles. Let t = <DOB = <EOC, and note that <DOE = 180 - t, <COD = <DOE. Then, using the area formula, we have the four equations. Note that sin(t) = sin(180 - t). Then: 3 = (1/2)(a)(x)sin(t), 4 = (1/2)(b)(y)sin(t), 6 =((1/2)(x)(y)sin(180 -t) = (1/2)(x)(y)sin(t), and Y = (1/2)(a)(b)sin(180 - t) = (1/2)(a)(b)sin(t). Then 2Y/8 =a/y, and 6/12 =a/y, so Y = 4. (I know you can't use the formula for obtuse angles, but this problem really brings it out; it is hardly ever mentioned). Ed Gray
Log in to reply
If 8 2 Y = y a = 1 2 6 then Y = 2 .
A bigger fallacy is that a quadrilateral is not a triangle. Please forgive the occasional lapse of an old man. With apologies, Ed Gray
Good !!!!!!!!!!!! I like it.
Yes, your solution to solve this problem is a way to proof Menelaus' Theorem
Log in to reply
Hi, Can you please tell us How ADE becomes ADC and BDE becomes BDC, Your solution is perfect but I couldnot understand the end although I know it is Happy End !!! THanks
F is the intersection of CD & BE.
The calculation of the yellow area is shown on the diagram itself.
It is interesting to note that if the triangle is to be formed then b²>ac.
please identify 'F'
Log in to reply
F is the intersection of CD & BE. The calculation of the yellow area is shown on the diagram itself. It is interesting to note that if the triangle is to be formed then b²>ac. F is where DC crosses BE I do believe
the first ratio should be AB/DB =(x+c)/9
Let the big triangle be denoted by ABC (A at the top , B at left , C at right)
Let the triangle of area 6 be denoted by OBC
Let the triangle of area 4 be denoted by OCD
Let the triangle of area 3 be denoted by OBE
Let the area of triangle ADO be x
Let the area of triangle AEO be y
In triangle AEC
y/(x + 4) = 3/6
Then
2y = x + 4 ........................................... (1)
In triangle ADB
x/(y + 3) = 4/6
Then
2y = 3x - 6 ............................................(2)
From (1), (2)
x= 5, y = 4.5
The area of the yellow region = 5 + 4.5 = 9.5
even i did the same thing
x
4
=
3
+
x
+
y
1
0
(This was the crux move in proving
Ceva's Theorem.
)
Similarly, y 3 = 4 + x + y 9
Now, solve these equations. We get, x = 5 and y = 4 . 5 .
Therefore, area of the yellow quadrilateral= x + y = 9 . 5
Moderator note:
To clarify, the equation is deduced by the ratio of triangles with the same base-line (without needing to resort to Ceva's Theorem). It can be used to prove Ceva's Theorem.
Dear Ritvik simply superb
have done just like you
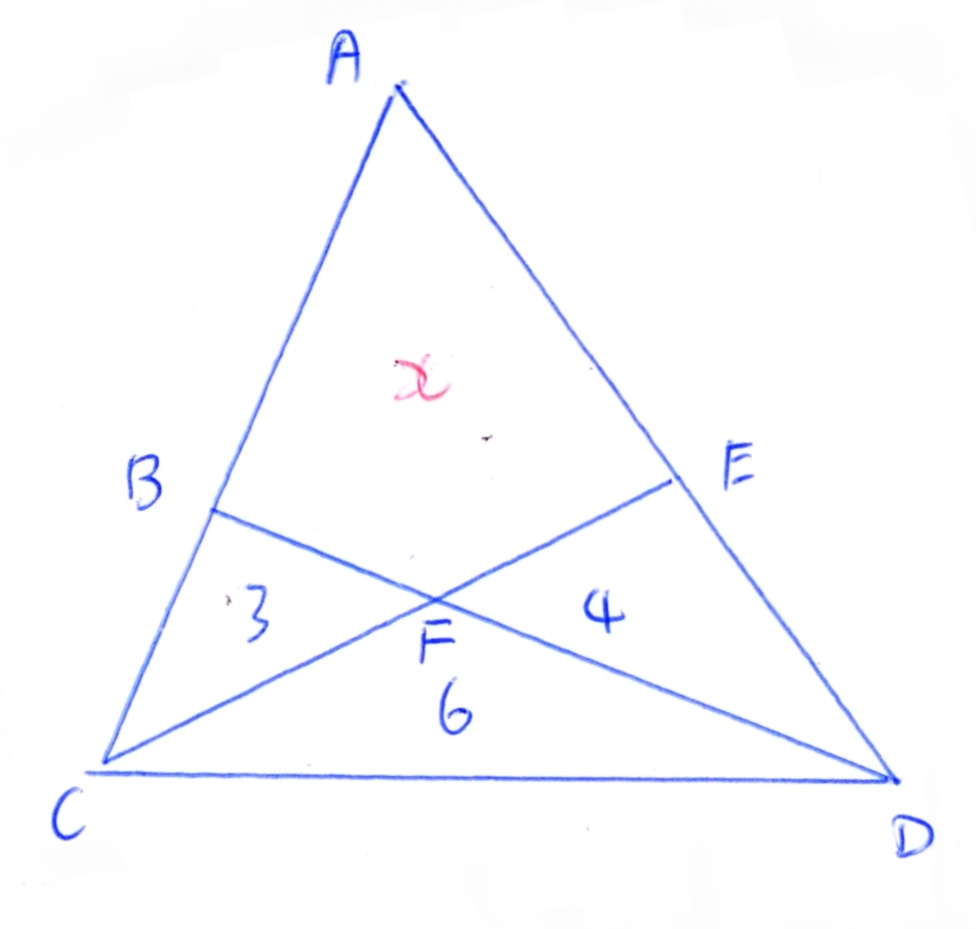
Let x = ( A B F E ) . By Menelaus' theorem, we have C B A C ⋅ F D B F ⋅ E A F E = − 1 in which C B A C = − ( D C B ) ( D C A ) = − 9 1 3 + x , and F D B F = ( C F D ) ( C F B ) = 2 1 , and E A D E = ( C E A ) ( C E D ) = x + 3 1 0 .
That is, we have − 9 x + 1 3 ⋅ 2 1 ⋅ x + 3 1 0 = − 1 Solving this equation yields ( A B F E ) = x = 9 . 5 as required.
How did you deduced the coordinates of (0,2) and similarly others
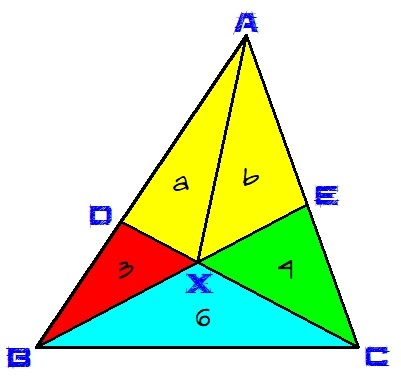 Consider the diagram. Recall that the areas of triangles with equal altitudes are proportional to the bases of the triangles. We have,
D
B
A
D
=
A
C
D
B
A
C
D
A
=
A
X
D
B
A
X
D
A
Consider the diagram. Recall that the areas of triangles with equal altitudes are proportional to the bases of the triangles. We have,
D
B
A
D
=
A
C
D
B
A
C
D
A
=
A
X
D
B
A
X
D
A
3 + 6 a + b + 4 = 3 a ⟹ 3 ( a + b + 4 ) = 9 a ⟹ a + b + 4 = 3 a ⟹ b + 4 = 2 a ( 1 )
E C A E = A B E C A A B E = A E X C A A X E
4 + 6 a + b + 3 = 4 b ⟹ 4 ( a + b + 3 ) = 1 0 b ⟹ 2 a + 2 b + 6 = 5 b ⟹ 2 a + 6 = 3 b ( 2 )
Substitute ( 1 ) in ( 2 ) , we have
b + 4 + 6 = 3 b ⟹ 1 0 = 2 b ⟹ 5 = b
It follows that,
2 a = b + 4 = 5 + 4 = 9 ⟹ a = 4 . 5
Finally, the area of the yellow region is a + b = 4 . 5 + 5 = 9 . 5
We can skew the triangle without affecting areas. Thus I work in this triangle:
We know the areas of three triangles with based A B . The areas are proportional to the heights, so that r : s : t : y = 6 : 9 : 1 0 : A , where A is the area of the entire triangle, which is 13 more than the yellow area.
From similar triangles, A B Q B = r s = 9 6 ∴ A B A Q = 3 1 ; also, A R A Q = t s = 1 0 6 ∴ A B A R = A Q A R ⋅ A B A Q = 6 1 0 ⋅ 3 1 = 9 5 . This gives B R / A B = ( A B − A R ) / A B = 1 − 9 5 = 9 4 , and a third pair of similar triangles shows 1 0 A = t y = B R A B = 4 9 , from which follows A = 2 2 2 1 and the yellow area is 2 2 2 1 − 1 3 = 9 2 1 .
I do not understand why AQ/QR=s/t
Log in to reply
My bad-- should be A Q / A R . I'll fix it in my solution.
Which short approach did you used can you elaborate plz with proof?



Who needs Menelaus? (On the other hand, the following might actually be essentially Menelaus' theorem rediscovered. I'm not good in geometry.)
Label the points as follows:
Denote the area of D E O as x , and the area of A D E as y .
Observe that using B E as the base, B O D and E O D has the same height, and thus the ratio of their areas is the ratio of their bases. That is, [ E O D ] [ B O D ] = E O B O , or x 3 = E O B O .
By observing B O C and E O C , we also get [ E O C ] [ B O C ] = E O B O , or 4 6 = E O B O . Equating the two equations gives x 3 = 4 6 , or x = 2 .
Using the same method, now with A B as the base, we have [ B D E ] [ A D E ] = B D A D = [ B D C ] [ A D C ] , or 3 + 2 y = 3 + 6 y + 2 + 4 . This gives y = 7 . 5 .
The area of the yellow region is thus x + y = 2 + 7 . 5 = 9 . 5 .