Yet Another Area Problem (Try 2 - I did not square something that needed squaring)
This problem's question: What is the area of the irregular heptagon?
If you worked the previous version, then you might have computed the correct answer.
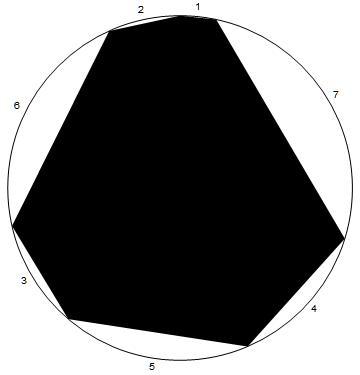
The sides are as indicated just outside the circle. They are all positive integers. You will have to numerically compute some equivalent to the circle's radius.
The answer is 54.7249466221096.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I gave you an interesting upvote. Our methodologies are not that dissimilar. You used half of the apex angles and I used the full apex angles to generate the radius computation equation. You used an Excel spreadsheet and I used a root finder to solve our preceding equations to get the numeric radius. You used Heron's formula, which avoids computing the triangles' altitudes and I computed the triangles' altitudes. We both summed the triangles' areas. I also used this procedure to check the area.
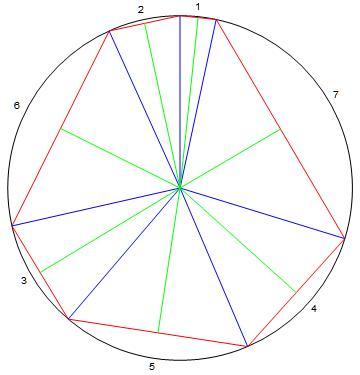
The radius is approximately 4.74753725744023.
The area is approximately 54.7249466221096, which was computed to the same answer by two different methods.
Also, I checked the Euclidean distance between vertices.
The red and blue lines show the sides of isosceles triangles. The green lines show the altitudes of the isosceles triangles.
The apex angles:
1 2 6 3 5 4 7 1 2 . 0 9 0 9 ∘ 2 4 . 3 1 9 2 ∘ 7 8 . 3 8 1 9 ∘ 3 6 . 8 3 6 7 ∘ 6 3 . 5 5 0 5 ∘ 4 9 . 8 2 9 7 ∘ 9 4 . 9 9 1 ∘
The methodology: compute the apex angles with the radius being an variable r , solving the resultant trigonometric equation to determine the radius and then summing the areas of the isosceles triangles using the now known radius to compute the green altitudes of the isosceles triangles. A little more work was done to check the result and to draw the answer illustration.
For those who can follow Wolfram Mathematica:
sides = { 2 , 6 , 3 , 5 , 4 , 7 , 1 }
angles = Table [ 2 cos − 1 ( r r 2 − ( 2 side ) 2 ) , { side , sides } ]
r = r /. FindRoot [ Evaluate [ Plus @@ angles ] = 2 π , { r , 5 . } ]
r is now known.
area = Plus @@ Table [ 2 1 side r 2 − ( 2 side ) 2 , { side , sides } ]
the area is now known
Let the radius of the circle be r , and the internal angle opposite side with length k be θ k , where k = 1 , 2 , 3 , ⋯ 7 .
Then we have r = 2 sin ( 2 θ k ) k and k = 1 ∑ 7 θ k = 2 π , ⟹ k = 1 ∑ 7 2 θ k = k = 1 ∑ 7 sin − 1 ( 2 r k ) = π , Solving for r numerically (I solved it with a simple Excel spreadsheet; see below), we get r ≈ 4 . 7 4 7 5 3 7 2 5 7 .
Let the area of the isosceles triangle with base length k be A k . Then area of the heptagon is:
A heptagon = k = 1 ∑ 7 A k = k = 1 ∑ 7 s k ( s k − r ) 2 ( s k − k ) = 4 1 k = 1 ∑ 7 k 4 r 2 − k 2 ≈ 5 4 . 7 2 5 Using Heron’s formula where s k = 2 2 r + k
Reference: Heron's formula