A calculus problem by neelesh vij

Let's generalize these for any $k>1$ .

Say $\displaystyle S=\sum_{m,n\ge1}\frac{m^2n}{k^m(mk^n+nk^m)}=\sum_{m,n\ge1}\frac{n^2m}{k^n(mk^n+nk^m)}$

We get by adding $\displaystyle 2S = \sum_{m,n\ge1} \frac{mn\cancel{(mk^n+nk^m)}}{k^{m+n}\cancel{(mk^n+nk^m)}}$

$\displaystyle 2S=\sum_{m,n\ge1}\frac{mn}{k^{m+n}}=\sum_{m=1}^{\infty}\frac{m}{k^m}\sum_{n=1}^{\infty}\frac{n}{k^n}$

A further generalization says $\displaystyle \sum_{m=1}^{\infty}\frac{m}{k^m} = \frac{k}{(k-1)^2}$ putting which we get ,

$\displaystyle 2S = \frac{16}{81}\implies \boxed{81S=8}$

Treating m and n as identical and different and replacing m with n and n with m we get

Adding the two series we get an AGP Which can be easily evaluated

i would like to write it clearly ... 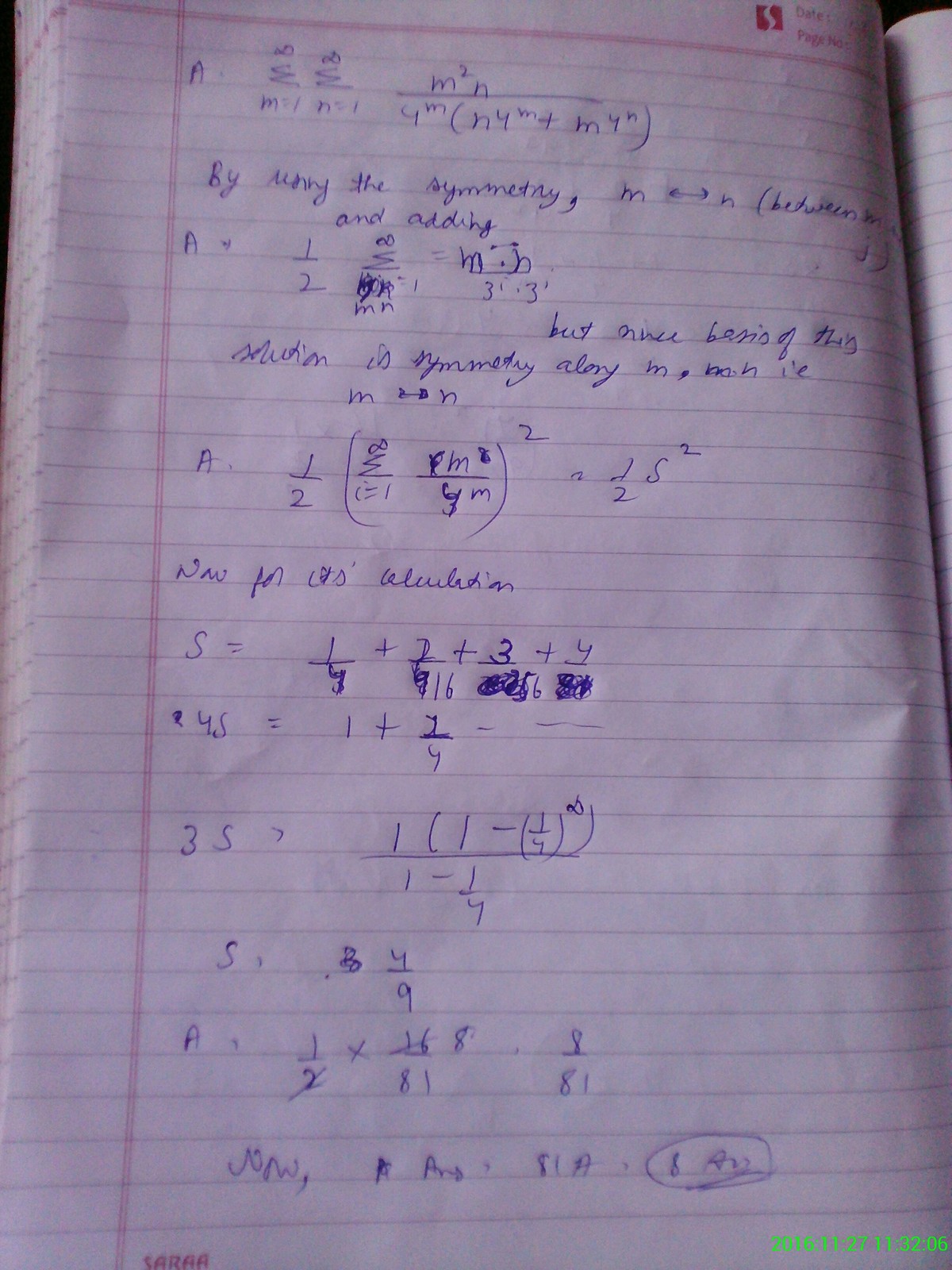here is a generalisation..