Yet another structure of cubes
 Some unit cubes can together form a structure, such as in the cover image above, or such as
this
or
this
problem. The cubes are ordered just as if they are
voxels
, and gravity takes effect downward (so no cubes can be floating), but otherwise there's no restriction.
Some unit cubes can together form a structure, such as in the cover image above, or such as
this
or
this
problem. The cubes are ordered just as if they are
voxels
, and gravity takes effect downward (so no cubes can be floating), but otherwise there's no restriction.
This time, you don't know the structure! You left the structure for lunch break, and when you returned, it's gone. You managed to take a picture of the structure, though. In fact, you don't only have one picture; you have three. You took:
- one from the front of the structure (top side is the direction up, right side is the direction right),
- one from the right side of the structure (top side is the direction up, right side is the direction back), and
- one from above of the structure, looking down (top side is the direction back, right side is the direction right).
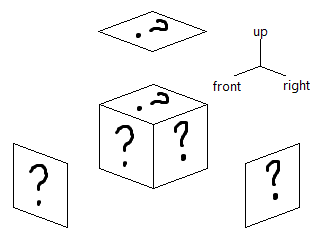
However, much to your surprise, when you look at the pictures they are all exactly the same!
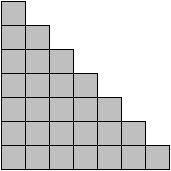
If and are respectively the minimum and maximum possible number of cubes in the structure, determine the value of .
Image shamelessly stolen from here .
The answer is 54.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
https://brilliant.org/problems/yet-another-structure-of-cubes/
First, to preserve my sanity, let's convert images to something more friendly. Consider the following example structure:
The above structure is viewed slightly off from perfectly above the structure. This shows how the structure is composed of stacks; nonexistent stacks are simply stacks of height 0 (marked asterisk below). This also allows us to represent the above succinctly as a single matrix of their heights:
⎝ ⎛ 1 3 3 2 1 2 2 ∗ 3 ⎠ ⎞
Call the above matrix as the height matrix of the example structure. Thus, for our problem, the height matrix of our structure will be this, for some positive integers a i j :
⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ a 1 1 a 2 1 a 3 1 a 4 1 a 5 1 a 6 1 a 7 1 ∗ a 2 2 a 3 2 a 4 2 a 5 2 a 6 2 a 7 2 ∗ ∗ a 3 3 a 4 3 a 5 3 a 6 3 a 7 3 ∗ ∗ ∗ a 4 4 a 5 4 a 6 4 a 7 4 ∗ ∗ ∗ ∗ a 5 5 a 6 5 a 7 5 ∗ ∗ ∗ ∗ ∗ a 6 6 a 7 6 ∗ ∗ ∗ ∗ ∗ ∗ a 7 7 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
Now, what restrictions do the two pictures from the front and from the right give?
However, instead of deducing the structure from the pictures, it's better to do the other way around first: given the structure, what are the pictures? Given the example structure above, what is the picture from the front? From the right? Let's fix our attention to the one from the front first, since the two are actually similar (rotating the structure allows the right side to be the front side).
First, observe that when looking from the front, gravity affects the situation: all cubes must be supported. Any higher cubes must be supported with lower cubes. Thus actually we can represent a front picture with a single vector, the heights of the stacks in order.
Next, each column is precisely the visible cubes in the column. But we can claim that this is also the height of the highest stack in the column, for that reason: if there's a higher stack, then some of its high cubes (higher than what's in the picture) would be visible; if there's no stack of that height, then the highest cube in the picture shouldn't have been there. For example, a column of 3 in the picture means there's a stack of height 3 and none higher; if there's one higher, than their 4th-level cube would be visible in the picture, while if there's none of height 3, then there would be no stack that shows a 3th-level cube.
Thus we can now easily construct the front picture of the example structure: it's simply ( 3 2 3 ) , the maximum number in each column. What about the right picture? It's similar, but we need to be careful: it's the maximum number in each row, but read from bottom to up, giving ( 3 3 2 ) . You can verify that the above structure indeed gives the following pictures:
Thus, our front and right picture vectors are the same ( 7 6 5 4 3 2 1 ) , which means:
Now our task is simpler. We have 2 8 variables a 1 1 , … , a 7 7 , each of which taking a positive integer value, and we also have the 1 4 equalities above. We need to determine max ∑ a i − min ∑ a i .
Let's find the maximum first. This is far easier. a i j is involved in two equalities: max { a 7 j , a 6 j , … } = 8 − j and max { a i 1 , a i 2 , … } = i . Thus a i j ≤ 8 − j and a i j ≤ i , or a i j ≤ min { 8 − j , i } . We can simply compute all 2 8 inequalities to give this matrix, where each nonzero entry is the maximum height of the stack there:
⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 1 2 3 4 5 6 7 ∗ 2 3 4 5 6 6 ∗ ∗ 3 4 5 5 5 ∗ ∗ ∗ 4 4 4 4 ∗ ∗ ∗ ∗ 3 3 3 ∗ ∗ ∗ ∗ ∗ 2 2 ∗ ∗ ∗ ∗ ∗ ∗ 1 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
Conveniently, this structure is also a valid structure! We can check that they indeed give the required pictures. Since we already have the maximum possible height for each stack, we also have the maximum possible sum for everything, which is 1 0 6 cubes.
Now we need to find the minimum. We have a few necessities: the first column and the last row must have a stack of height 7, the second column and the second-last row must have a stack of height 6, and so on. For some of these, we can actually satisfy both simultaneously: we can simply set a 7 1 = 7 to satisfy both the first column and the last row criteria, a 6 2 = 6 to satisfy the second column and the second-last row, and similarly a 5 3 = 5 , a 4 4 = 4 . However, we cannot do so for the two 3-stack equalities: the fifth row and the third column don't have any intersection (it must be empty), so we're forced to have two 3-stacks. Likewise, we have two 2-stacks. The remaining stacks are at least 1 cube high, since they are positive integers. Note that this is also optimal: we need one 7-stack, one 6-stack, one 5-stack, one 4-stack, two 3-stacks, two 2-stacks, and the rest at least 1 cube each, for the described reasons (satisfy criteria, some criteria intersecting at no stack, etc). They total up to 5 2 cubes:
⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 1 1 1 1 1 1 7 ∗ 2 1 1 1 6 1 ∗ ∗ 3 1 5 1 1 ∗ ∗ ∗ 4 1 1 1 ∗ ∗ ∗ ∗ 3 1 1 ∗ ∗ ∗ ∗ ∗ 2 1 ∗ ∗ ∗ ∗ ∗ ∗ 1 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
This gives a difference of 1 0 6 − 5 2 = 5 4 .