Yin Yang
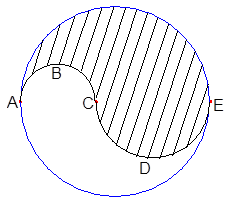 Diameter ACE is divided at C in the ratio 2:3 The two semicircles, ABC and CDE, divide the circular region into an upper (shaded) region and a lower region. The ratio of the area of the upper region to that of the lower region can be expressed as
b
a
, where
a
and
b
are coprime positive integers. What is the value of
a
+
b
?
Diameter ACE is divided at C in the ratio 2:3 The two semicircles, ABC and CDE, divide the circular region into an upper (shaded) region and a lower region. The ratio of the area of the upper region to that of the lower region can be expressed as
b
a
, where
a
and
b
are coprime positive integers. What is the value of
a
+
b
?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Someone reported this problem wrong.
Log in to reply
The report stated "It does not say to find the sum of a and b at the end." which is a valid clarification. I've since updated your question to reflect asking for a + b .
Let
A u = Area upper region
A l = Area lower region
A t = Total area
Assume the radius of the circle is r = 1 0 .
A u = 2 5 2 π − 2 2 2 π + 2 3 2 π = 1 5 π
A l = A t − A u = 5 2 π − 1 5 π = 1 0 π
A l A u = 1 0 π 1 5 π = 2 3
a + b = 3 + 2 = 5
To simplify calculations, let the formula f ( d ) of the area of a semicircle given diameter d be f ( d ) = c d 2 for a constant c .
We see that the area of the black region is 2 5 c + 9 c − 4 c = 3 0 c and the area of the white region is 2 5 c + 4 c − 9 c = 2 0 c .
Thus the ratio is 2 0 c 3 0 c = 2 3 so our answer is 3 + 2 = 5 .