You are supposed to solve this (part 3)
Source: Geogebra
I have a metal rectangle sheet, when looked sideway, it looks like this:

The width of the sheet, i.e., the length of
is 1. I want to bend it such that it makes an isosceles trapezoid
(without the base AB), like this:
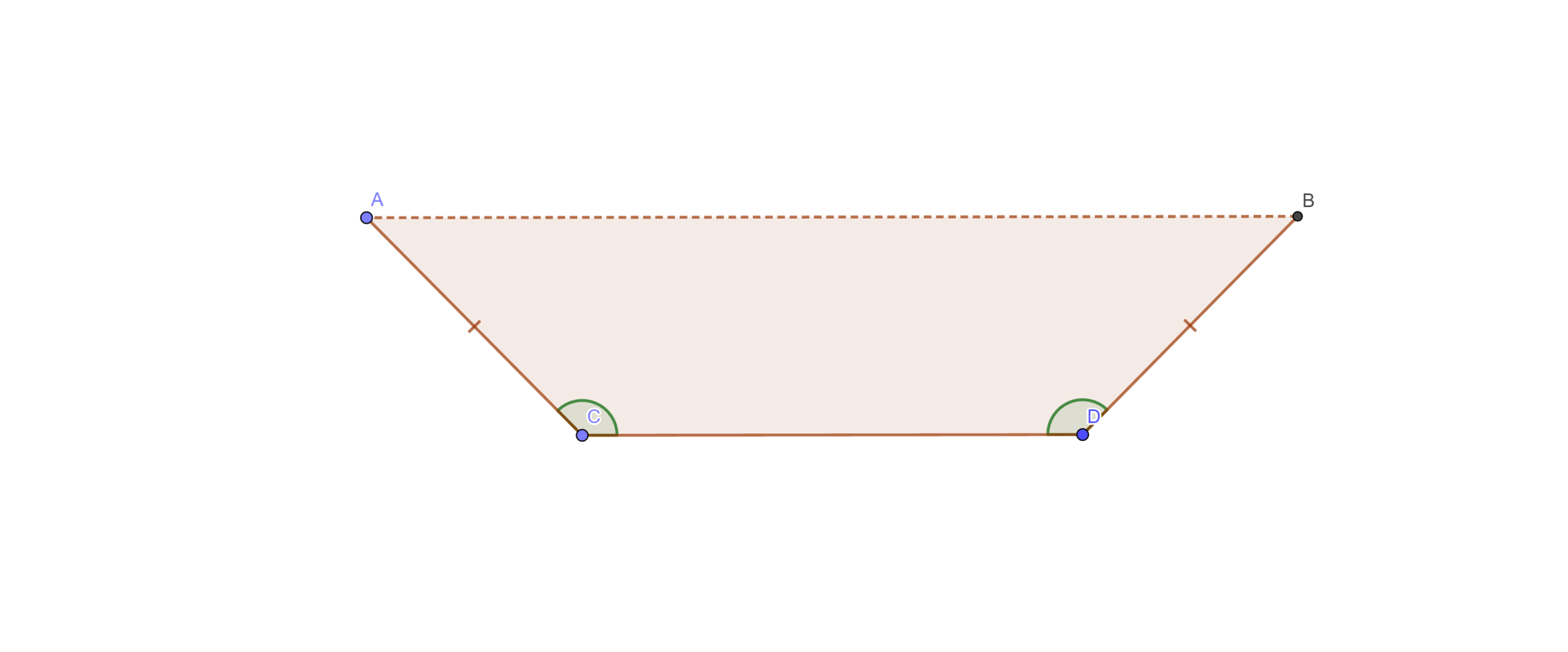
Let be such that and are positive integers and is an irreducible fraction and be degree. Given that the area of has reached its maximum (and the total length of , and is equal to the length of , assuming when bending the sheet, there is no distortion in length), what is the value of ?
Don't try to measure using the shape given, it has not reached its maximum (the correct shape is in the solution).
The answer is 360.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Source: Geogebra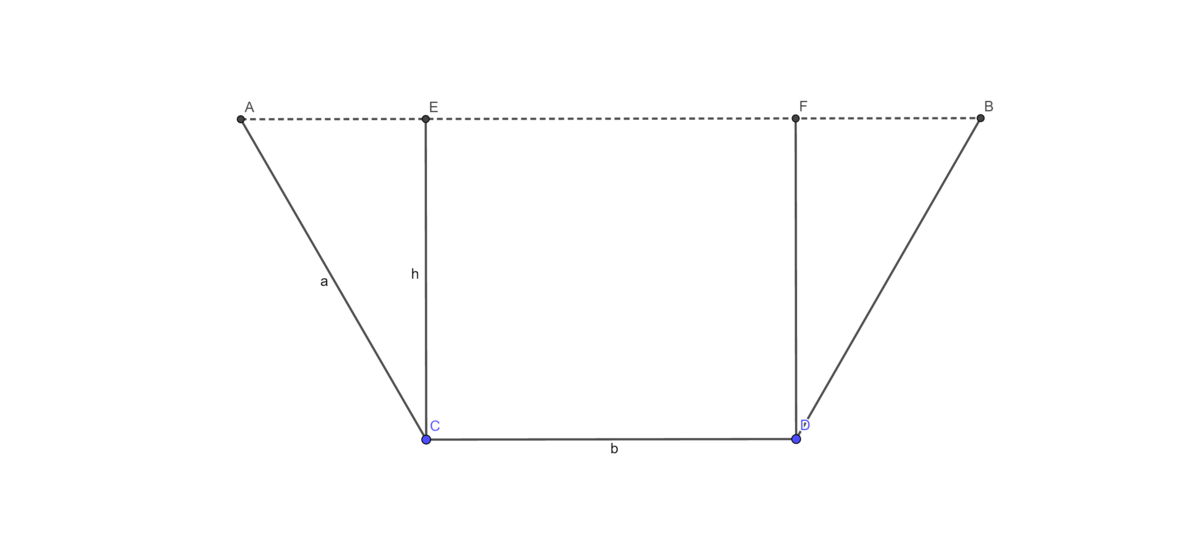
Let C E and D F be 2 altitudes of the trapezoid A C D B . Let S be the area of the trapezoid A C D B . c Let the side A C be a , the base C B be b , the altitude C E be h and A E be t . Notice that the total length of A C , C D , and D B is equal to the length of XY. Hence, we have: 2 a + b = 1 .
Consider the triangle △ A C E , applying the Pythagoras theorem, we have:
A E 2 = A C 2 − E C 2
⇒ h 2 = a 2 − t 2
⇒ h = a 2 − t 2
Notice that C E / / D F (since they are both the altitudes of the trapezoid ACDB) and A B / / C D (since they are both the bases of the trapezoid ACDB), hence E F D C is a parallelogram ⇒ { E F = C D = b C E = D F .
Consider △ A C E and △ B D F , applying the Pythagoras theorem, we have:
{ A E 2 = A C 2 − E C 2 B F 2 = B D 2 − D F 2
Moreover, we had { A C = B D C E = D F .
From that, we can conclude that B F = A E = t
The area of the trapezoid A C D B is:
S = 2 ( A B + C D ) C E
⇒ S = 2 ( A E + E F + F B + b ) h
⇒ S = ( t + b ) a 2 − t 2
⇒ S 2 = ( t + b ) 2 ( a 2 − t 2 )
⇒ S 2 = ( t + b ) 2 ( a − t ) ( a + t )
⇒ 3 S 2 = ( t + b ) ( t + b ) ( 3 a − 3 t ) ( a + t )
Applying the A M − G M inequality with 4 positive numbers: t + b , t + b , 3 a − 3 t , a + t , we have:
⇒ 3 S 2 ≤ ( 4 ( t + b ) + ( t + b ) + ( 3 a − 3 t ) + ( a + t ) ) 4
⇒ 3 S 2 ≤ ( 2 2 a + b ) 4
⇒ 3 S 2 ≤ ( 2 1 ) 4
⇒ S 2 ≤ 4 8 1
⇒ S ≤ 1 2 3 .
The equality holds if and only if t + b = 3 a − 3 t = a + t
⇒ { a = b 2 a = 4 t
⇒ { 3 a = 1 a t = 2 1
⇒ { a = 3 1 A C A E = 2 1
⇒ { A C = 3 1 sin ( ∠ A C E ) = 2 1
⇒ { y x = 3 1 ∠ A C E = 3 0 °
⇒ ⎩ ⎪ ⎨ ⎪ ⎧ x = 1 y = 3 ∠ A C D = 1 2 0 °
⇒ ⎩ ⎪ ⎨ ⎪ ⎧ x = 1 y = 3 z = 1 2 0
⇒ x y z = 3 6 0 .
We have our final answer: 3 6 0 .