You call it Time period I call it a Question
Find the fundamental period of f ( t ) = ∣ sin t ∣ + ∣ cos t ∣ .
Note : A function has a period of T if f ( t ) = f ( t + T ) for all t . The fundamental period is the smallest positive period.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Since sine and cosine have both periods 2 π , that case is trivial.
To prove period π we can use identities ( ∀ x ∈ R ) sin ( x ) = − sin ( x + π ) and cos ( x ) = − cos ( x + π ) as follows: f ( t + π ) = ∣ sin ( t + π ) ∣ + ∣ cos ( t + π ) ∣ = ∣ − sin ( t ) ∣ + ∣ − cos ( t ) ∣ = ∣ sin ( t ) ∣ + ∣ cos ( t ) ∣ = f ( t )
To prove the π / 2 case we use angle addition identities and known values of sine and cosine for π / 2 : f ( t + 2 π ) = ∣ ∣ ∣ sin ( t + 2 π ) ∣ ∣ ∣ + ∣ ∣ ∣ cos ( t + 2 π ) ∣ ∣ ∣ = ∣ ∣ ∣ cos ( 2 π ) sin ( t ) + sin ( 2 π ) cos ( t ) ∣ ∣ ∣ + ∣ ∣ ∣ cos ( 2 π ) cos ( t ) − sin ( 2 π ) sin ( t ) ∣ ∣ ∣ = ∣ 0 sin ( t ) + 1 cos ( t ) ∣ + ∣ 0 cos ( t ) − 1 sin ( t ) ∣ = ∣ sin ( t ) ∣ + ∣ cos ( t ) ∣ = f ( t )
π / 4 answer can be proven wrong by counterexample e. g. knowing that sin ( π / 4 ) = cos ( π / 4 ) = 2 / 2 we have
f ( 0 + 4 π ) f ( 0 ) = ∣ ∣ ∣ sin ( 0 + 4 π ) ∣ ∣ ∣ + ∣ ∣ ∣ cos ( 0 + 4 π ) ∣ ∣ ∣ = 2 2 2 = 2 = = ∣ sin ( 0 ) ∣ + ∣ cos ( 0 ) ∣ = 1 Hence it can't be true that ( ∀ t ∈ R ) f ( t + π / 4 ) = f ( t ) and the answer is π / 2 .
GOOD SOLUTION BUT IS THERE ANY OTHER
By definition, the period is the minimum value of T such that f(t)=f(t+T), for all t. Therefore, T=π/2.
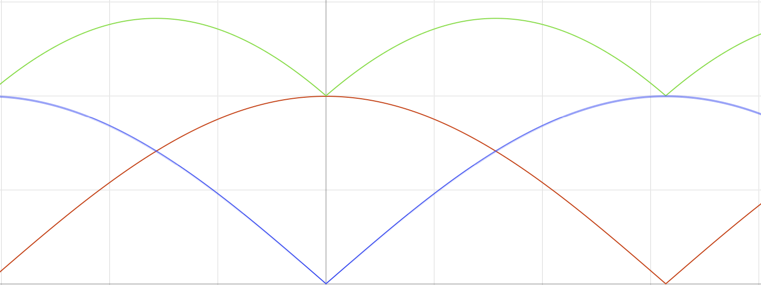
sin t and cos t have periods of 2 π
∣ sin t ∣ and ∣ cos t ∣ have periods of π
But their sum has a period of π / 2 . Can someone explain why?
I didn't explain why and didn't prove there is not a smaller period than π / 2 (and have no idea how to prove it) but I have proven it to be smallest of the possible answers. Check out my answer.
yes, Dale gray has proved it correctly.
Let f(x)=|sin x|+|cos x|. Then,
Therefore, if it can be shown that T=π/2 is the least positive number satisfying f(x+T)=f(x), then the period of f is π/2. Suppose that f(x+T)=f(x), with 0<T<π/2. Then,
Squaring both sides in Eq.(1) and simplifying, using cos²θ+sin²θ=1 and sin(2θ)=2sinθcosθ, gives
Squaring both sides in Eq.(2) gives
or
after factoring the difference of two squares. Setting the first factor in Eq.(4) equal to zero, gives
which means that 2T is a multiple of the period, π, of the function x↦sin(2x). Therefore, 2T=nπ for some positive integer n. But this contradicts the assumption that 0<T<π/2. Setting the second factor in Eq.(4) equalto zero, gives
Using the trigonometric identity
in Eq.(5) gives
Therefore,
The first choice in Eq.(7) is not possible since cosT is positive when 0<T<π/2. The second condition in Eq.(7) implies that T is a multiple of the period, π, of the function x↦sin(2x), giving
again contradicting the assumption that 0<T<π/2. Therefore, π/2 is the smallest positive number satisfying f(x+T)=f(x). Therefore the period of f is π/2. This was typed using Scientific Workplace and copied and pasted here. There seems to be some incompatibility issue in the way the two environments handle LATEX.