You can be the king kong banging on your chest

Geometry Level 2

In the figure ,square ABCD has side length 2 .A semicircle with AB as diameter is constructed inside the square ,and the tangent to the semicircle from C intersects AD at E ,then the length of CE i 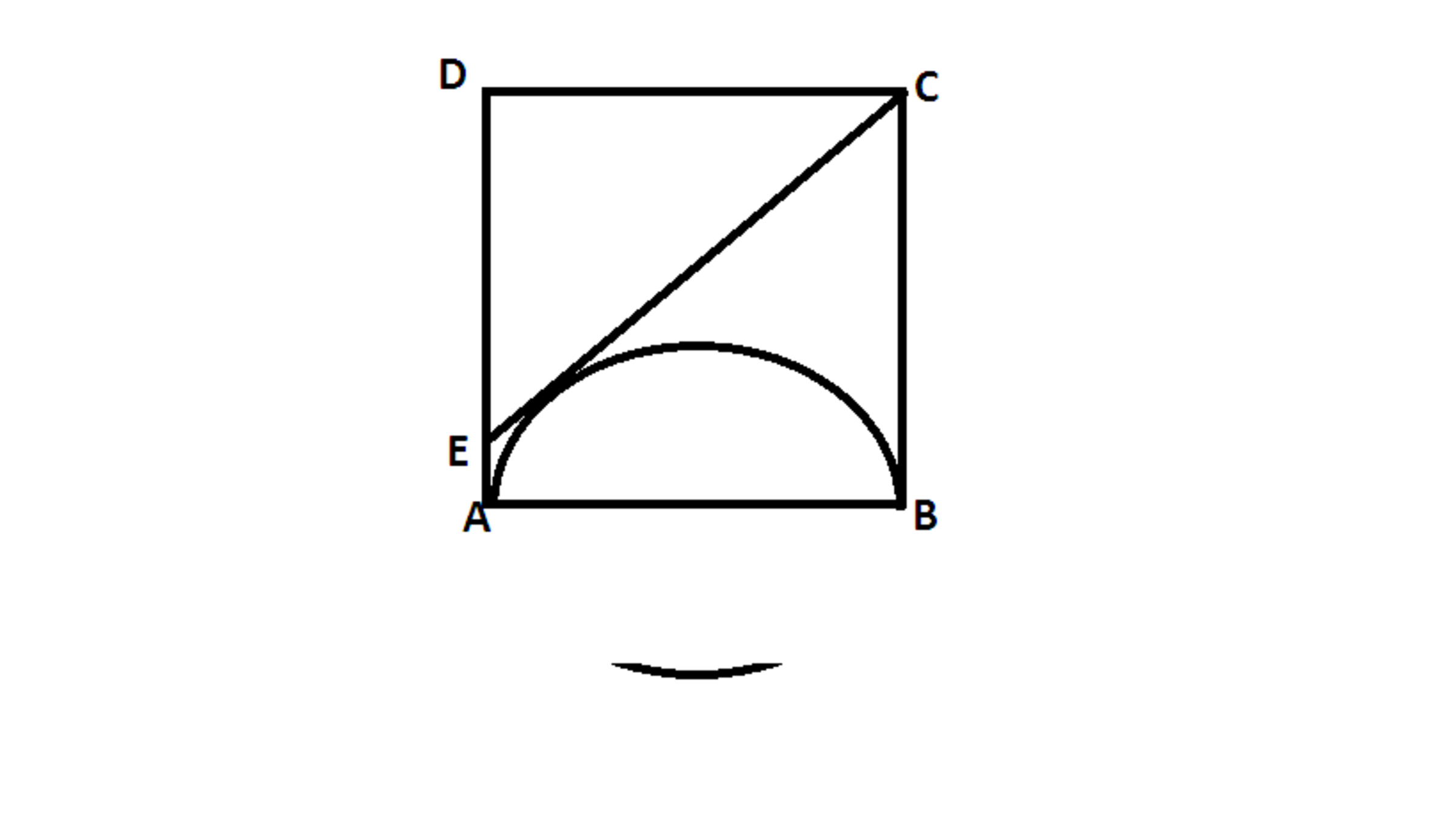s


The answer is 2.5.

Raven Herd by Raven Herd , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Marta Reece
Aug 19, 2017

∡ E C D = 9 0 ∘ − 2 × arctan ⁡ 1 2 ≈ 36.8 7 ∘ \measuredangle ECD=90^\circ-2\times \arctan\frac12\approx36.87^\circ

E C = 2 cos ⁡ 36.8 7 ∘ = 2.5 EC=\dfrac2{\cos36.87^\circ}=\boxed{2.5}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

I attempted the coordinate geometry approach

Let the center of the semi-circle be the origin (0,0)

Equation of the semi-circle is : X^2+y^2=1 (y >=0)

Diff, 2x + 2yy’ = 0

Y’=-2x/2y =-x/y = slope of tangent to the semi-circ at the point of intersection (x,y)

Equation of tangent line from C

y-y1 = m(x-x1)

Coordinates of C : (1,2)

y-2=-(x/y)*(x-1)

y(y-2)=-x(x-1) ' y^2-2y=-x^2+x

x+2y=1

Now E is the intersection of the above line with the vertical line x=-1 Substituting x = -1 in the above, we get y=1

E=(-1,1)

L[CE] = Distance between C & E = sqrt((1-(-1))^2 + (1-2)^2)

= sqrt(2^2+1)

= sqrt(5)

= 2.236068

What is wrong with this line of reasoning ?

Sundar R - 3 years, 9 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...