A geometry problem by Raven Herd
In the figure ,radius of incircle of ABC is 4 cm.If BD =6 cm ,DC = 8 cm then the length of AC is!
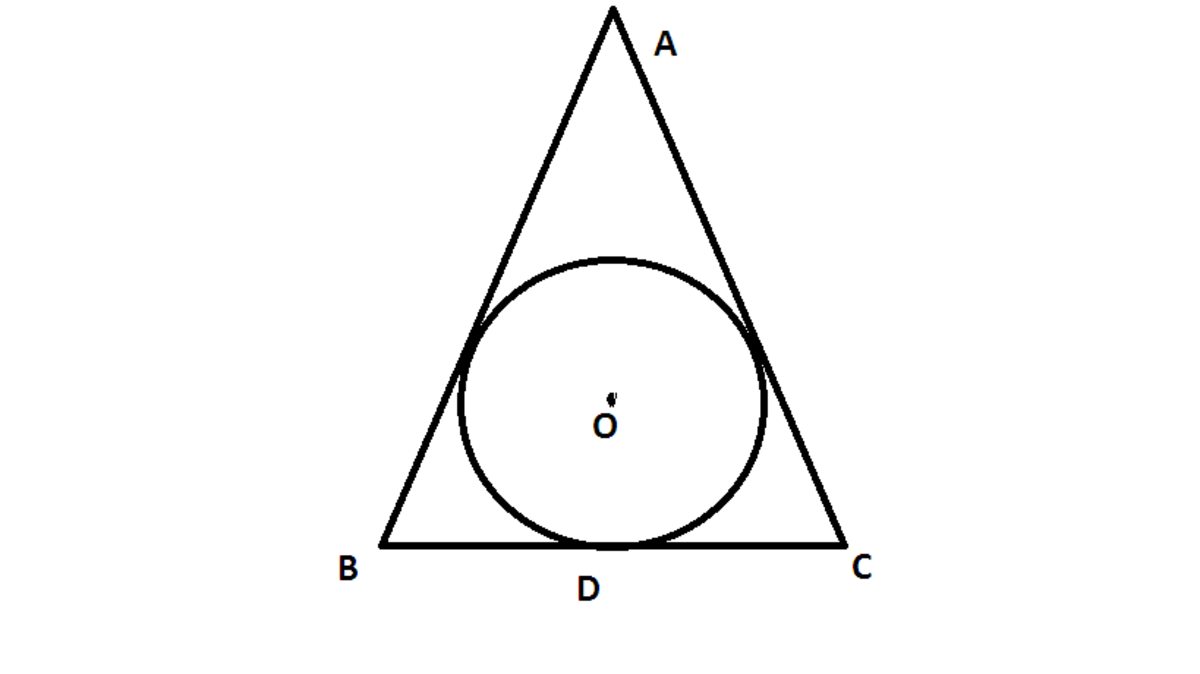
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
∡ O C D = arctan 8 4 ≈ 2 6 . 5 6 ∘
∡ O B D = arctan 6 4 ≈ 3 3 . 6 9 ∘
∡ B A C = 1 8 0 ∘ − 2 × ∡ O C D − 2 × ∡ O B D ≈ 5 9 . 4 9 ∘
Distance from A to point tangent to the incircle = t a n 2 5 9 . 4 9 4 = 7
A C = 7 + 8 = 1 5
It would be helpful if point D was identified as the point at which the incircle is tangent to the side BC. It would be even better if the triangle did not appear to be isosceles, but that would take more doing.
Assume that the in-circle touches AB, AC in E & F resply and that AE=AF=x. Then the semi-perineter,s = x +14 and the area of Tr. ABC = A =4(x+14). Also by Heron's formula, A =((x+14)(8)(x)(6))^(1/2) or 4(x+14)=((x+14)(8)(x)(6))^(1/2) which yields, x = 7 or -14. Hence, AC = 7 + 8 =15 cm.