You can solve it!!
There is a square ABCD and an equilateral triangle ABE,such that E,C,D are points on a circle,find the radius of this circle if the diagonal of the square is equal to under root two.
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
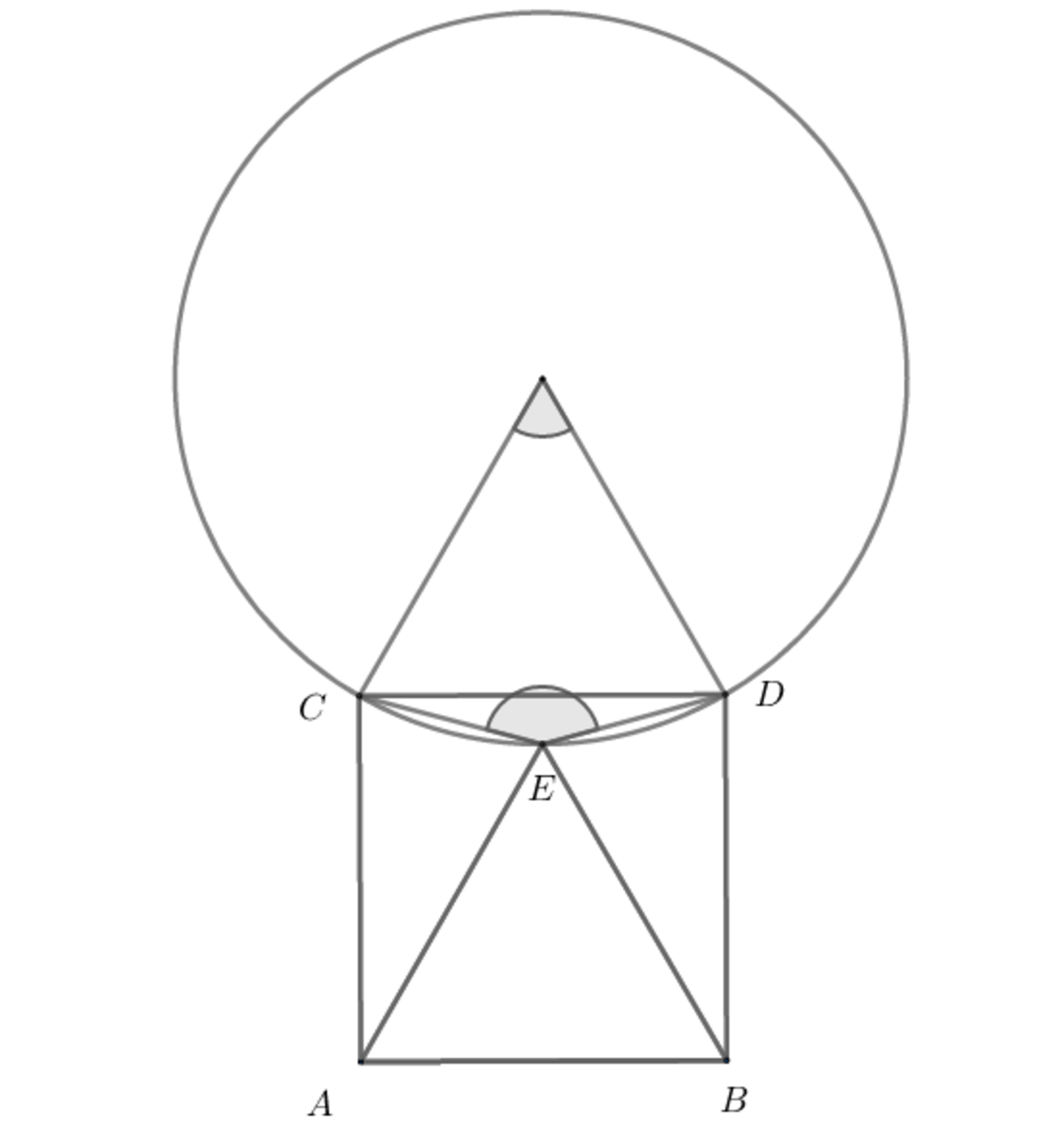 ∠
C
E
D
=
1
5
0
∘
hence major arc
C
D
=
3
0
0
∘
and
∠
C
O
D
=
6
0
∘
∠
C
E
D
=
1
5
0
∘
hence major arc
C
D
=
3
0
0
∘
and
∠
C
O
D
=
6
0
∘
That makes △ O C D equilateral hence radius is 1
We can place the problem in the coordinate plane, with A = ( 0 , 0 ) , B = ( 1 , 0 ) , C = ( 0 , 1 ) , D = ( 1 , 1 ) . .
E forms and equilateral triangle with A and B , so E = ( 2 1 , ± 2 ( 3 ) ) . Interestingly, these cases give the same result, and I will only give the example of E = ( 2 1 , 2 3 ) .
We now have C = ( 0 , 1 ) , D = ( 1 , 1 ) , E = ( 2 1 , 2 3 ) are on the same circle. The center of the circle must be equidistant from C and D so the x-coordinate of the center must be 2 1 .
Now, using the distance formula, we set the distance from the center to C equal to the distance to E:
2 1 2 + ( y − 1 ) 2 = ( y − 2 3 ) 2
4 1 + y 2 − 2 y + 1 = y 2 − 3 + 4 3
( 2 − 3 ) y = 2 1
y = 2 1 2 − 3 1 = 2 2 + 3
The distance from the center to E is just 2 2 + 3 − 2 3 = 1
based from the problem the diagonal of the square will become the legs of the right triangle that will be formed. The hypotenuse is equal to the radius of the circle.