You could beat the world
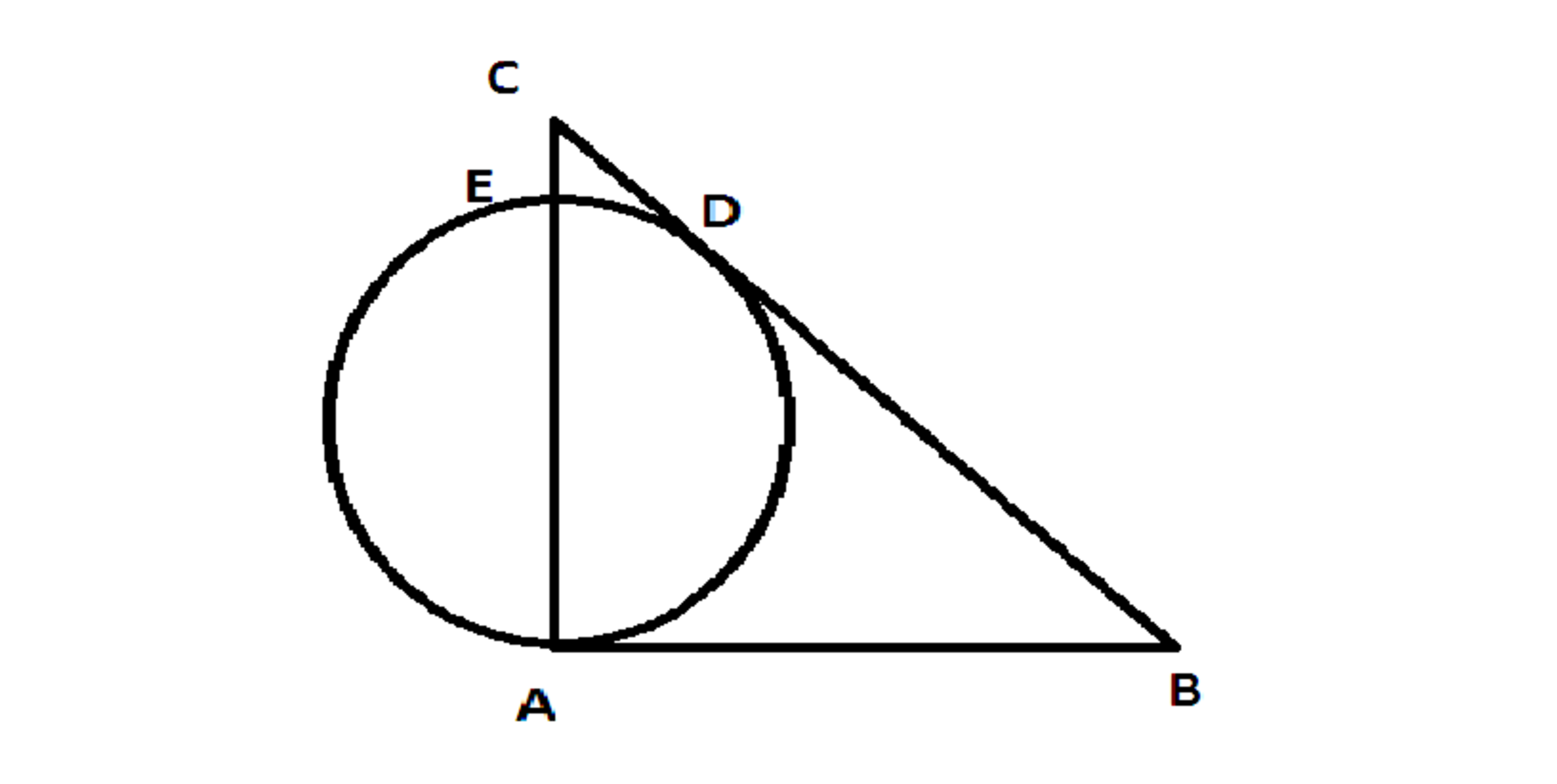
is a right triangle with . Let a circle tangent to at and tangent to to some point . Suppose the circle intersects again at and the cm, cm, what is ?
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
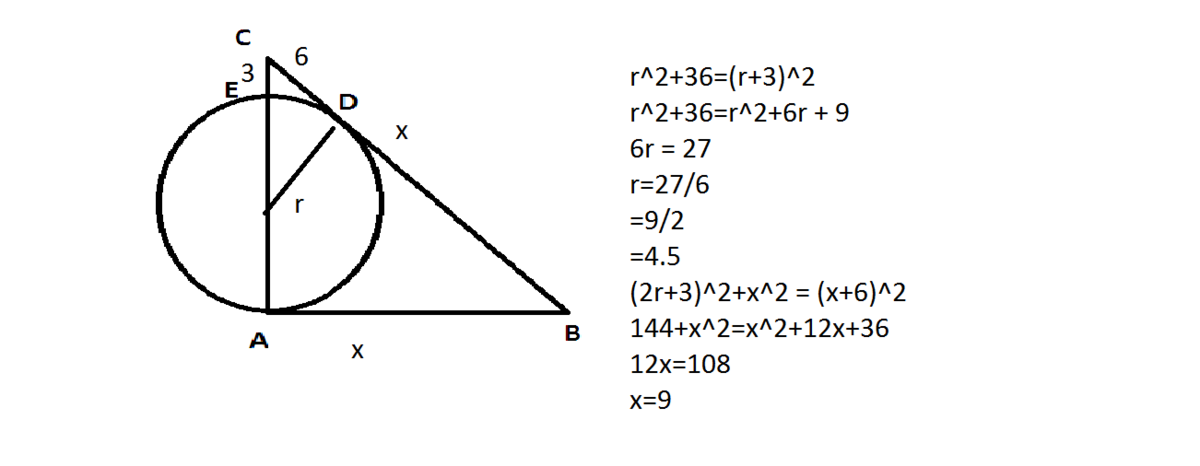
Since angle C D O is right,
6 2 + r 2 = ( 3 + r ) 2
3 6 + r 2 = 9 + 6 r + r 2
6 r = 2 7
r = 4 . 5 c m
By similar triangles,
3 + r 6 = 6 + B D 3 + r + r , paying close attention to what goes on the numerator and the denominator , since, as evidenced by the diagram, the two triangles are orientated differently to one another.
3 + 4 . 5 6 = 6 + B D 3 + 4 . 5 + 4 . 5
Cross-multiplying,
3 6 + 6 B D = 9 0
6 B D = 5 4
B D = 9 c m