A Slim Right Triangle
Triangle A B C is right angled at C . A D splits ∠ B A C in the ratio 2 : 1 , where ∠ C A D is smaller.
If A C = 2 and C D = 1 , find the length of B D .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Yeah the very same method.
Given: AC=2, BC=1
In ∆ACD tanx=
A
C
C
D
=
2
1
........(1.)
 Using sine rule and equating AD in triangles ACD and ADB:
sin
x
C
D
=
cos
3
x
×
sin
2
x
B
D
Using sin2x=2(sinx)(cosx) and cos3x=
4
cos
3
x
−
3
cos
x
BD=
4
cos
2
x
−
3
2
=
1
+
tan
2
x
4
−
3
2
=
1
0
(
U
s
i
n
g
(
1
.
)
)
Using sine rule and equating AD in triangles ACD and ADB:
sin
x
C
D
=
cos
3
x
×
sin
2
x
B
D
Using sin2x=2(sinx)(cosx) and cos3x=
4
cos
3
x
−
3
cos
x
BD=
4
cos
2
x
−
3
2
=
1
+
tan
2
x
4
−
3
2
=
1
0
(
U
s
i
n
g
(
1
.
)
)
Let's chuck this triangle on to the Argand plane, with A being the origin. Thus, C = 2 and D = 2 + i . We also have that ∠ C A D is 3 1 ∠ C A B . Thus,
3 ar g D = ar g B
ar g D 3 = ar g B
D 3 = B
( 2 + i ) 3 = B
B = 2 + 1 1 i
From this, we get B C = 1 1 , which implies B D = 1 0 .
Construct D ′ on C B such that C D ′ = C D = 1 and D ′ = D . Since A C ⊥ D D ′ , A C perpendicularly bisects D D ′ and thus △ D ′ A D is isosceles, which implies ∠ D A D ′ = 2 ∠ C A D = ∠ D A B . By Pythagorean Theorem A D ′ = 5 and by angle bisector theorem A B D B = A D ′ D D ′ = 5 2
Applying Pythagorean Theorem on A B C : 4 + ( D B + 1 ) 2 = A B 2 .
By substitution: B D 2 − 8 B D − 2 0 = ( B D − 1 0 ) ( B D + 2 ) = 0 ⟹ B D = 1 0 .
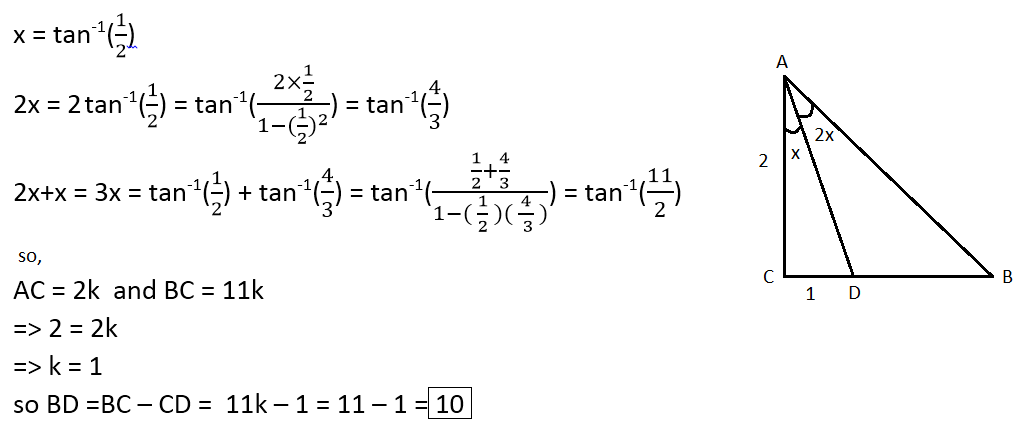
Let ∠ C A D = θ , then ∠ B A D = 2 θ and ∠ B A C = 3 θ .
We note that:
A C B C ⇒ B C ⇒ B D = tan ∠ B A C = tan ( 3 θ ) = 1 − 3 tan 2 θ 3 tan θ − tan 3 θ We also note that tan ∠ C A D = tan θ = A C C D = 2 1 = 1 − 4 3 2 3 − 8 1 = 2 1 1 = A C × tan θ = 2 × 2 1 1 = 1 1 = B C − C D = 1 1 − 1 = 1 0