You don't need 4 equations.

Add and subtract $10a+14b+22c$ to the left side . Then Turn the right side to the left side .

You'll get :- $a^2+b^2+c^2+519+10a+14b+22c-10a-14b-22c-d-36\sqrt{10a+14b+22c-d}=0$

Complete to perfect squares:- $(a^2-10a+25)+(b^2-14b+49)+(c^2-22c+121)+((10a+14b+22c-d)-36\sqrt{10a+14b+22c-d}+324)=0$

So , $(a-5)^2+(b-7)^2+(c-11)^2+( \sqrt{10a+14b+22c-d} -18)^2=0$

So we will get that $a=5,b=7,c=11$ and $\sqrt{10a+14b+22c-d}=18$ , so $390-d=18^2=324$ ,

$\boxed{d=66}.$

The situation is that of a sphere of radius $\sqrt{195}$ , the diagonal of a $5\times 7\times 11$ box, centered at $\left\{22 \sqrt{\frac{15}{13}}-5,154 \sqrt{\frac{3}{65}}-7,242 \sqrt{\frac{3}{65}}-11\right\}$ tangent with an infinite plane at $\left\{22 \sqrt{\frac{15}{13}},154 \sqrt{\frac{3}{65}},242 \sqrt{\frac{3}{65}}\right\}$ . The origin, the sphere's center and the point of tangency are all in a straight line. The normal vector of the infinite plane is parallel to that straight line.

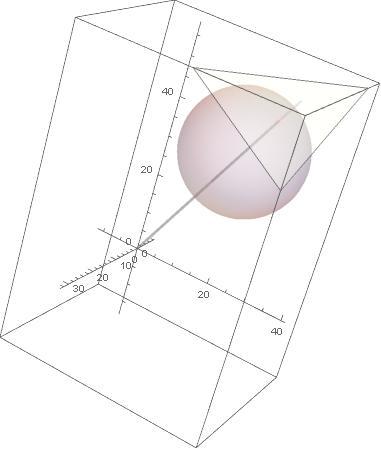
My actual solution was solve $a^2+b^2+c^2+519=36 \sqrt{10 a+14 b+22 c-d}+d$ for $d$ getting $\pm36 \sqrt{-a^2+10 a-b^2+14 b-c^2+22 c-195}+a^2+b^2+c^2-129$ and minimizing that expression to get $\{66,\{a\to 5,b\to 7,c\to 11\}\}$ .

It took me longer to reconstruct the original situation.

Using the functions $f(a,b,c)=a^2+b^2+c^2+519$ and $g(a,b,c)=5a+7b+11c$ , the problem writes as $f=d+36\sqrt{2g-d}$ , which can easily be rewritten as a quadratic polynomial in d: $d^2+(36^2-2f)d + f^2-36^2(2g)=0$ , which has solutions

$d=\frac{ (2f-36^2) \pm \sqrt{ (36^2-2f)^2-4( f^2-36^2(2g))} }{2}$ .

Rework this to $d=f-648 \pm 36\sqrt{324-f+2g}$ .

Now the problem suggests that we can find a unique value for d, so we are going to assume that the discriminant $D=324-(a^2+b^2+c^2+519)+2(5a+7b+11c)$ has maximum value 0. Setting the derivatives of this expression with respect to a, b and c to 0 we get $a=5, b=7, c=11$ , so that we find $g= 195$ and $f=714$ . Trying it out we find

$D = 324-f+2g= 324-714+2×195=0$ . The fact that this is indeed 0 justifies our earlier assumption.

Finally, $d = 714 - 648 = \boxed{66}$ .