You don’t need to know the side lengths
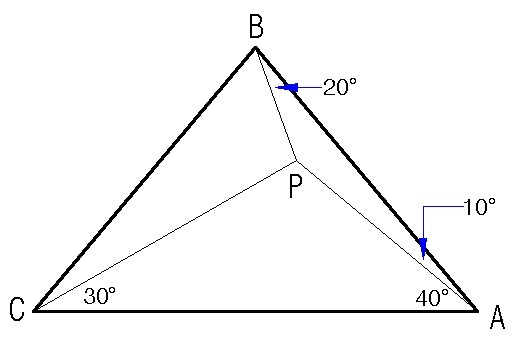 A point
P
is inside triangle
A
B
C
such that
∠
P
A
B
=
1
0
∘
,
∠
P
B
A
=
2
0
∘
,
∠
P
C
A
=
3
0
∘
, and
∠
P
A
C
=
4
0
∘
. Find
∠
P
C
B
in degrees.
A point
P
is inside triangle
A
B
C
such that
∠
P
A
B
=
1
0
∘
,
∠
P
B
A
=
2
0
∘
,
∠
P
C
A
=
3
0
∘
, and
∠
P
A
C
=
4
0
∘
. Find
∠
P
C
B
in degrees.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
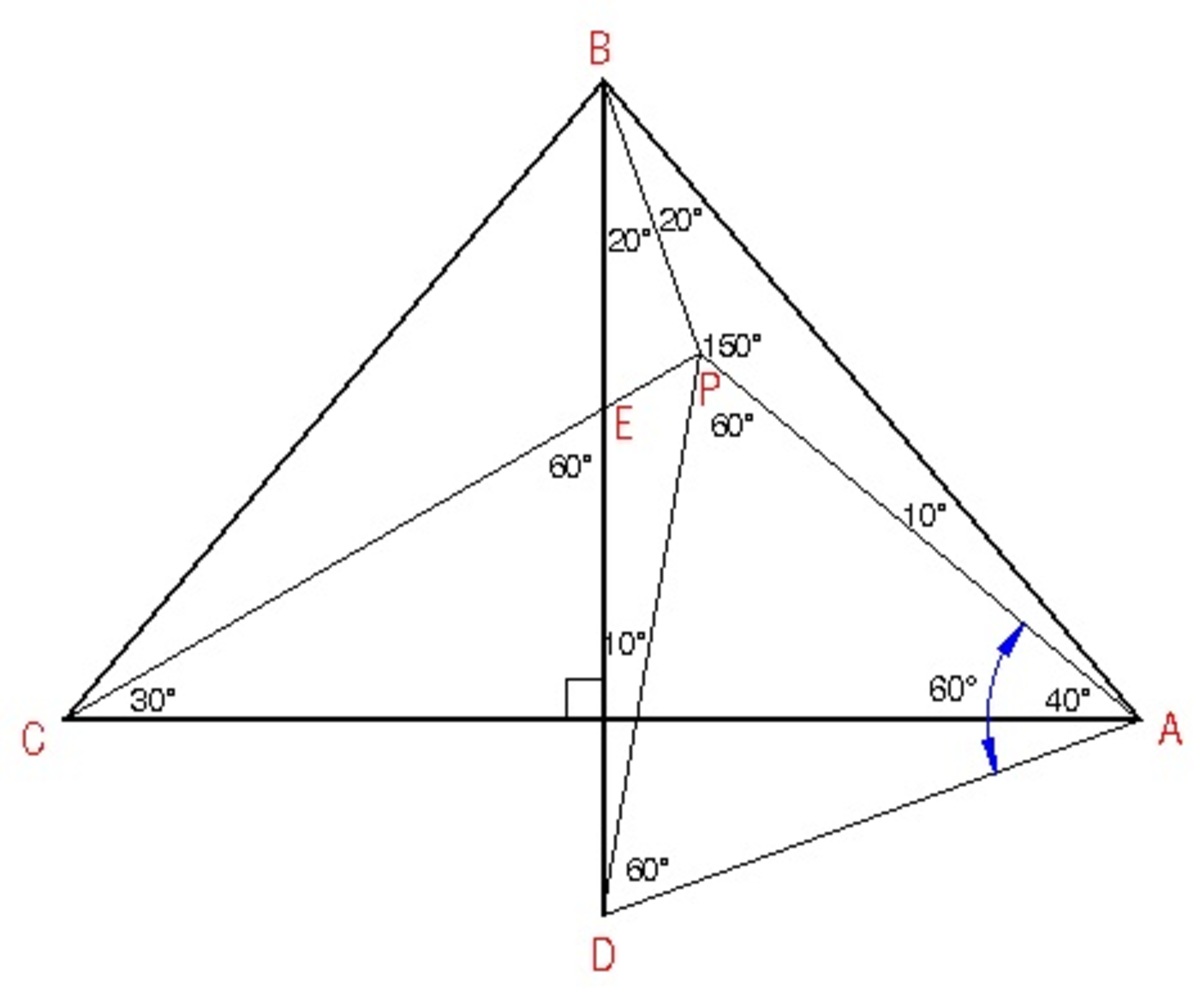 Let
D
be the reflection of
A
accross the line
B
P
. Then
∠
A
P
B
=
1
8
0
−
(
1
0
+
2
0
)
=
1
5
0
. Since
D
is a reflection of
A
accross the line
B
P
,
∠
P
B
D
=
∠
P
B
A
=
2
0
,
∠
B
P
D
=
∠
B
P
A
=
1
5
0
and
∠
P
D
B
=
∠
P
A
B
=
1
0
. Therefore,
∠
A
P
D
=
3
6
0
−
∠
B
P
D
−
∠
B
P
A
=
3
6
0
−
1
5
0
−
1
5
0
=
6
0
. Since
A
P
=
P
D
, triangle
A
P
D
is an equilateral triangle. Since
∠
B
A
C
=
5
0
and
∠
A
B
D
=
4
0
,
B
D
is perpendicular to
A
C
. Let
E
be the intersection of
B
D
and
A
C
.
∠
P
E
D
=
1
8
0
−
∠
C
E
D
=
1
8
0
−
(
9
0
−
3
0
)
=
1
2
0
. And so
∠
P
E
D
+
∠
D
A
P
=
1
8
0
. We conclude that quadrilateral
A
P
E
D
is a cyclic, and therefore
∠
D
E
A
=
∠
D
P
A
=
6
0
. Since
∠
A
E
D
=
∠
C
E
D
=
6
0
and
B
D
is perpendicular to
A
C
, we conclude that
A
B
=
B
C
. That means that
∠
A
C
B
=
5
0
. Finally.
∠
P
C
B
=
5
0
−
3
0
=
2
0
.
Let
D
be the reflection of
A
accross the line
B
P
. Then
∠
A
P
B
=
1
8
0
−
(
1
0
+
2
0
)
=
1
5
0
. Since
D
is a reflection of
A
accross the line
B
P
,
∠
P
B
D
=
∠
P
B
A
=
2
0
,
∠
B
P
D
=
∠
B
P
A
=
1
5
0
and
∠
P
D
B
=
∠
P
A
B
=
1
0
. Therefore,
∠
A
P
D
=
3
6
0
−
∠
B
P
D
−
∠
B
P
A
=
3
6
0
−
1
5
0
−
1
5
0
=
6
0
. Since
A
P
=
P
D
, triangle
A
P
D
is an equilateral triangle. Since
∠
B
A
C
=
5
0
and
∠
A
B
D
=
4
0
,
B
D
is perpendicular to
A
C
. Let
E
be the intersection of
B
D
and
A
C
.
∠
P
E
D
=
1
8
0
−
∠
C
E
D
=
1
8
0
−
(
9
0
−
3
0
)
=
1
2
0
. And so
∠
P
E
D
+
∠
D
A
P
=
1
8
0
. We conclude that quadrilateral
A
P
E
D
is a cyclic, and therefore
∠
D
E
A
=
∠
D
P
A
=
6
0
. Since
∠
A
E
D
=
∠
C
E
D
=
6
0
and
B
D
is perpendicular to
A
C
, we conclude that
A
B
=
B
C
. That means that
∠
A
C
B
=
5
0
. Finally.
∠
P
C
B
=
5
0
−
3
0
=
2
0
.
Let ∠ P C B = θ . We note that ∠ C P A = 1 8 0 ∘ − 3 0 ∘ − 4 0 ∘ = 1 1 0 ∘ and ∠ B P A = 1 8 0 ∘ − 1 0 ∘ − 2 0 ∘ = 1 5 0 ∘ , therefore, ∠ B P C = 3 6 0 ∘ − 1 1 0 ∘ − 1 5 0 ∘ = 1 0 0 ∘ and ∠ C B P = 1 8 0 ∘ − 1 0 0 ∘ − θ = 8 0 ∘ − θ . Now we can find θ using sine rule on △ C B P as follows:
B P sin θ = C P sin ( 8 0 ∘ − θ )
We only need to find B P and C P . Let A C = 1 . By sine rule:
sin 4 0 ∘ C P ⟹ C P sin 1 0 ∘ B P ⟹ B P = sin 1 1 0 ∘ 1 = sin 1 1 0 ∘ sin 4 0 ∘ = sin 2 0 ∘ A P = sin 1 1 0 ∘ sin 2 0 ∘ sin 3 0 ∘ sin 1 0 ∘ Note that A P = sin 1 1 0 ∘ sin 3 0 ∘
Now we have:
B P sin θ sin θ sin θ sin θ sin θ 4 sin 4 0 ∘ sin θ ⟹ tan θ ⟹ θ = C P sin ( 8 0 ∘ − θ ) = C P B P sin ( 8 0 ∘ − θ ) = sin 1 1 0 ∘ sin 2 0 ∘ sin 3 0 ∘ sin 1 0 ∘ × sin 4 0 ∘ sin 1 1 0 ∘ ( sin 8 0 ∘ cos θ − cos 8 0 ∘ sin θ ) = sin 1 1 0 ∘ sin 2 0 ∘ sin 3 0 ∘ sin 1 0 ∘ × sin 4 0 ∘ sin 1 1 0 ∘ ( sin 8 0 ∘ cos θ − cos 8 0 ∘ sin θ ) = 4 sin 4 0 ∘ cos θ − 4 sin 4 0 ∘ tan 1 0 ∘ sin θ = cos θ − tan 1 0 ∘ sin θ = 4 sin 4 0 ∘ + tan 1 0 ∘ 1 = 4 sin 2 0 ∘ sin 4 0 ∘ + sin 2 0 ∘ tan 1 0 ∘ sin 2 0 ∘ = 2 ( cos 2 0 ∘ − cos 6 0 ∘ ) + 2 sin 1 0 ∘ cos 1 0 ∘ × cos 1 0 ∘ sin 1 0 ∘ sin 2 0 ∘ = 2 cos 2 0 ∘ − 1 + 2 sin 2 1 0 ∘ sin 2 0 ∘ = 2 cos 2 0 ∘ − cos 2 0 ∘ sin 2 0 ∘ = tan 2 0 ∘ = 2 0 ∘
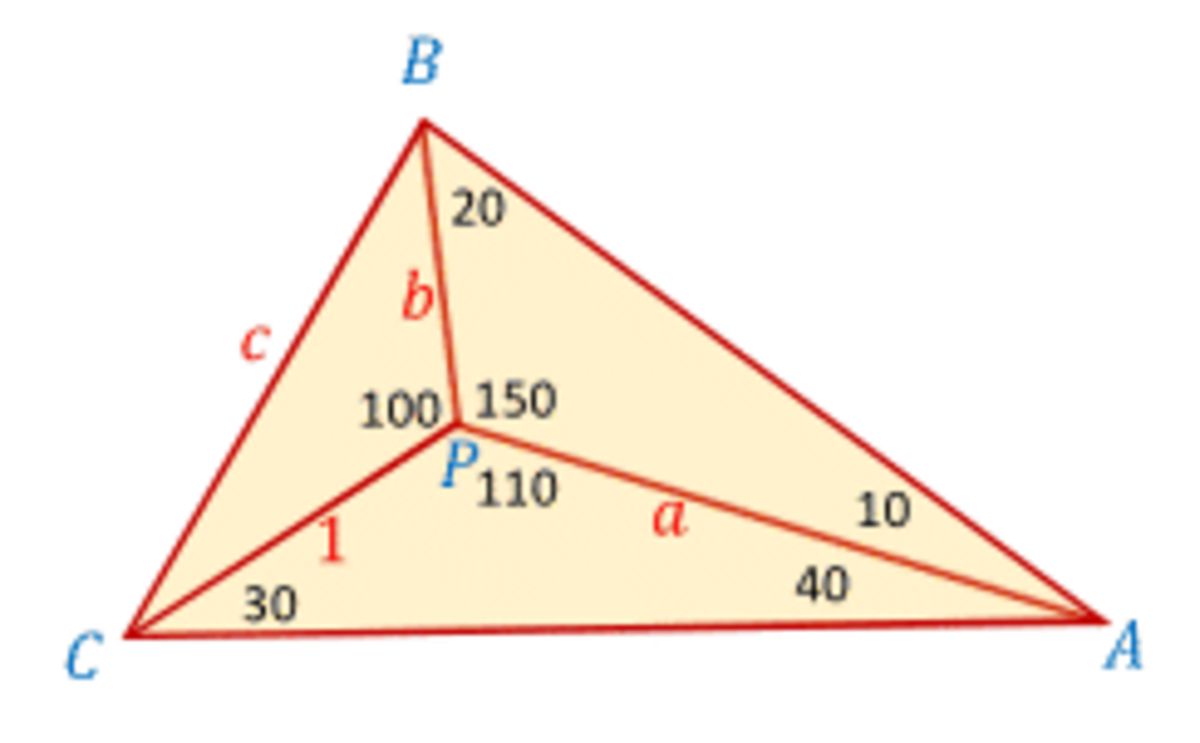 Angles easy to obtain are listed in image. Set
C
P
=
1
. Law of sines in
A
P
C
is
a
=
sin
(
3
0
)
sin
(
4
0
)
1
Angles easy to obtain are listed in image. Set
C
P
=
1
. Law of sines in
A
P
C
is
a
=
sin
(
3
0
)
sin
(
4
0
)
1
Law of sines in A P B gives b = sin ( 1 0 ) sin ( 2 0 ) a = sin ( 2 0 ) sin ( 1 0 ) sin ( 4 0 ) sin ( 3 0 ) = 0 . 3 9 4 9 3
Law of cosines in C P B gives us c = b 2 + 1 − 2 b cos ( 1 0 0 ) = 1 . 1 3 7 1 6
Law of sines in C P B finally results in ∠ B C P = arccos ( 2 c 1 + c 2 − b 2 ) = 2 0 ∘