Once Again, You Forgot The Radius!
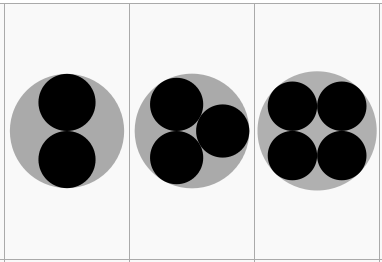
Three identical circles from left to right contain 2, 3, and 4 small circles, respectively, such that the small circles (identical in each group) are tangential to each other and to the large circle. The total area of the small circles is the largest for the small circles.
Image Credit: Wikimedia Koko90 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's find the ratio of areas between the two circles and the larger circle as shown in the left column given in the problem statement.
Let r 2 denote the radii of the two equal circles enclosed inside a circle with minimal radius R 2 .
The sum of diameters of the two small circles is equal to the diamater of the encompassing circle: 2 ( d 2 ) = R 2 ⇒ 2 ( 2 r 2 ) = 2 ( 2 R 2 ) ⇒ 2 r 2 = R 2 .
The area of the black region is equal to the sum of areas of the two small circles, π r 2 2 + π r 2 2 = 2 π r 2 2 .
The area of the grey region is equal to area of the encompassing circle minus the area of the small circles, π R 2 2 − 2 π r 2 2 = 4 π r 2 − 2 π r 2 2 = 2 π r 2 2 .
The ratio of areas between these two regions is 2 π r 2 2 π r 2 2 = 2 1 ( 1 ) .
Let's find the ratio of areas between the three circles and the larger circle as shown in the left column given in the problem statement.
Since we're finding the ratio of areas, we can assume that the radii of all three circles is r 3 = 1 .
Let O 1 , O 2 and O 3 denote the center of the three smaller circles, then O 1 O 2 O 3 is an equilateral triangle. Now let O 4 denote the center of this triangle, and let s = O 4 O 1 = O 4 O 2 = O 4 O 3 , then ∡ O 1 O 4 O 2 = ∡ O 1 O 4 O 3 = ∡ O 2 O 4 O 3 = 3 3 6 0 ∘ = 1 2 0 ∘ .
By cosine rule , 2 s 2 − 2 s 2 cos ( 1 2 0 ∘ ) = 2 2 ⇒ s = 3 4 . And so the radius of the encompassing circle, R 3 is equal to R 3 = s + r 3 = 3 4 + 1 .
Like above, taking the ratio of the two regions gives us π ( 3 4 + 1 ) 2 − 3 π 3 π ≈ 1 . 8 8 2 6 .
Let's find the ratio of areas between the four circles and the larger circle as shown in the left column given in the problem statement.
Since we're finding the ratio of areas, we can assume that the radii of all three circles is r 4 = 1 .
By joining the center of these four smaller circles, we get a square of side length 2 and diagonal 2 2 (By Pythagorean theorem ), thus the diameter of encompassing circle is 2 r 4 + 2 2 = 2 2 + 2 .
Likewise, we can work out the areas to be π ( 2 + 1 ) 2 − 4 π 4 π ≈ 2 . 1 8 .
Comparing these values show that the answer is 4.