Alternating Near Harmonic Series?
 4
×
[
1
−
3
1
+
5
1
−
7
1
+
…
]
=
?
4
×
[
1
−
3
1
+
5
1
−
7
1
+
…
]
=
?
Details and Assumptions :
-
π is the ratio of circumference to diameter of a circle.
-
G denote the Gravitational constant.
-
γ denote Euler-Mascheroni constant.
-
ℏ denote Planck constant.
Image Credit: Wikimiedia Apple Pie by Scott Bauer
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
good solution............thanks.
By approximation. The terms of the series are decreasing so the answer is somewhere between three and four. The gravitational constant is about ten, euler-mascheroni constant is about a half, pi is between three and four and the planck constant is about zero. So it has to be pi....
How come that expansion of t a n − 1 ( x 1 ) or c o t − 1 ( x 1 ) ?
Taylor Series
Just for those who aren't much familiar with taylor and mclaurin's theorem,they can follow this approach Let f(x)=1/1+x^2=(1+x^2)^(-1),,now expand using binomial theorem for any rational index to obtain f(x)=1-x^2+x^4-x^6+....... Now integrate both sides and put x=1,to obtain pi/4...which when multiplied by 4 gives us pi..:)
Python 2.7:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
|
Moderator note:
Because π is an irrational number, you have only shown that the series is approximately equals to π , when in fact you should prove that the series is in fact equals to π .
Oh man, I put in the oven for 35 seconds, then it displayed e . Now I know where's my error.
Insightful and analytical, best answer right here! +1
Lmao, I'm the
Martha Stewart
of mathematics.
 martha & snoop
martha & snoop

Bwahahahaha !!!!!!
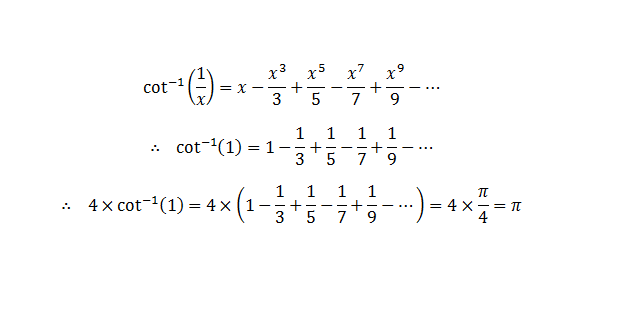
Thanks, Abhishek Ghosh for the nice solution. That would mean it will work with tan − 1 x too. Which is also more familiar to most people.
The Maclaurin series of tan − 1 x is as follows:
tan − 1 x = x − 3 1 x 3 + 5 1 x 5 − 7 1 x 7 + . . .
We know that:
tan − 1 1 = 4 π = 1 − 3 1 + 5 1 − 7 1 + . . .
⇒ π = 4 × ( 1 − 3 1 + 5 1 − 7 1 + . . . )