Mixing arithmetic and geometric progressions
Algebra
Level
3
Consider an increasing arithmetic progression, whose first term is 1 and 2nd , 10th and 34th are in a geometric progression.
Find the common difference of this arithmetic progression.
The answer is 0.33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
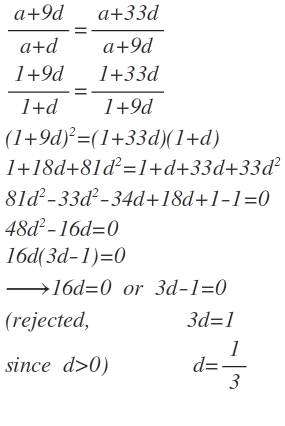
as 2nd 10th and 34th term of the A.P are in G.P
{a+(2-1)d} {a+(34-1)d}=[a+(10-1)d]^2
and we know that, a=1
so,
(1+d).(1+33d)=(1+9d)^2
1+d+33d+33d^2 = 1+81d^2 +18d
48d^2 - 16d=0
d(48d-16)=0
d=0,
d=16/48=1/3, d=1/3
But the question says that common difference is positive
So , d=0.33