You Must Construct Additional Pylons
Probability
Level
3
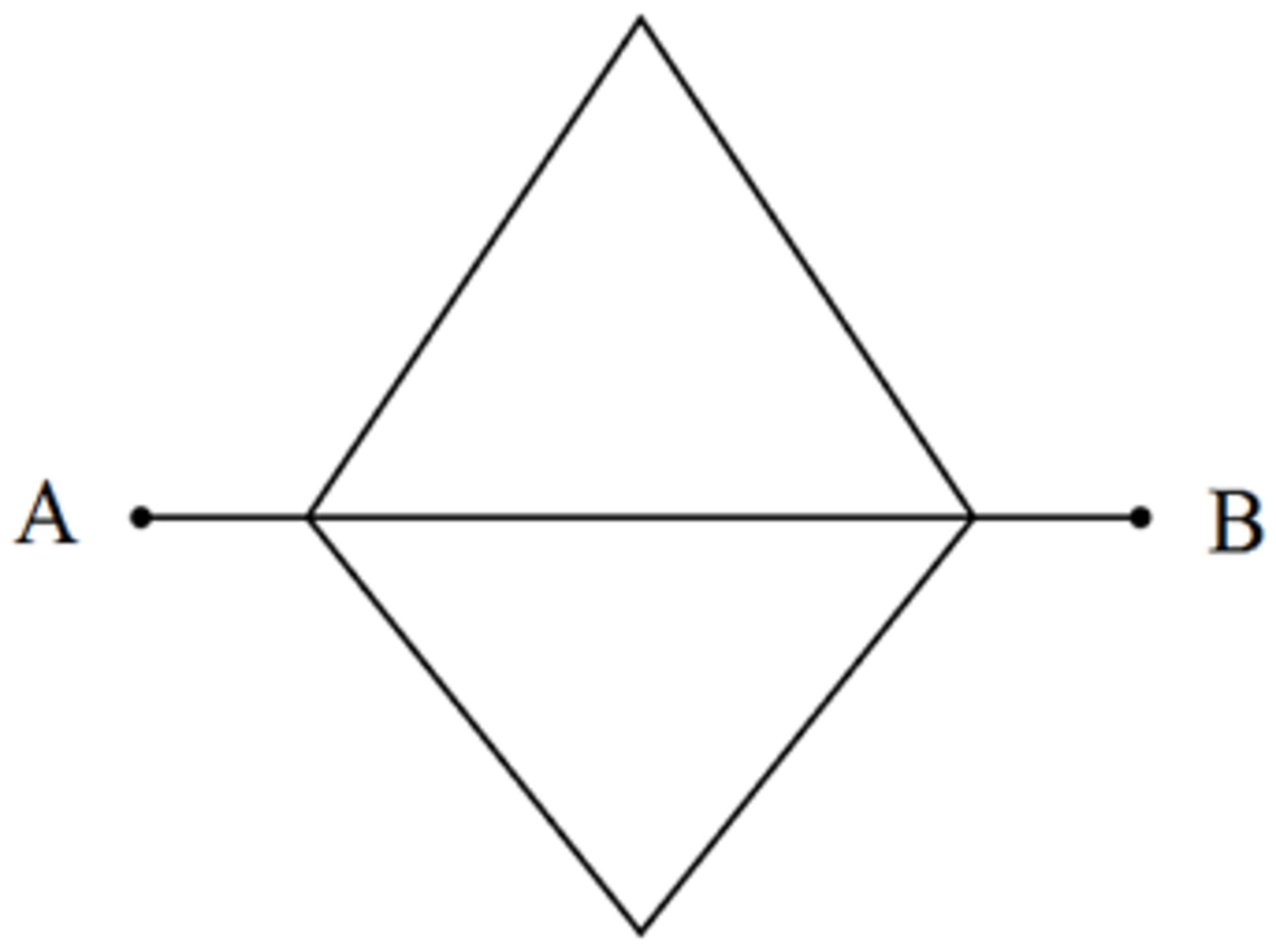
If I want to move from point A to point B, and I cannot traverse each edge more than once, how many paths could I possibly take?
5
7
9
11
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Notice that the exact shape of the path is irrelevant to the problem. We only need certain important points, precisely, the intersections. Let us relabel the diagram.
In total, there are 9 walks from A to B