You really need to be careful with this...
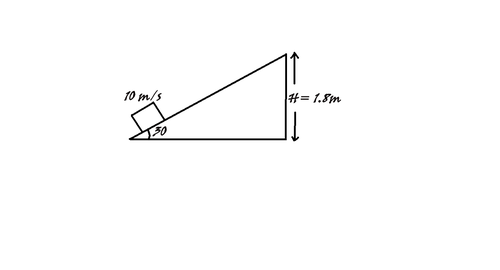 All surfaces are frictionless and wedge is fixed on the ground. A block of mass 1 Kg is given a velocity of 10m/s along the incline. The maximum height reached by the block from the ground level (in m) is :
All surfaces are frictionless and wedge is fixed on the ground. A block of mass 1 Kg is given a velocity of 10m/s along the incline. The maximum height reached by the block from the ground level (in m) is :
The answer is 2.6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Dont understand one thing ... vertical velocity is 5 m s − 1 , then highest height h = 2 × 9 . 8 5 2 = 1 . 2 7 5 5 What's wrong with my approach , considering this vertical way ? Please explain .
Log in to reply
same problem as me.. I approach the answer must 1.2755...
You're assuming the block will undergo projectile motion from the bottom of the wedge itself! But that's not possible (block can't go through the wedge). So, first block will reach top of the wedge and then projectile motion (free fall).
I agree with Samiur Rahman Mir.
It makes sense to only talk about the kinetic energy (which is 50J) and it's relation to distance. This is because E=Fd (in general), where 'd' is distance along which a force acts.
You can do this vertically in two ways, either you can resolve the force of gravity (9.81N/Kg) along the slope or use can resolve the velocity of the block in a vertical direction (because this will vary the working value of E). After all the only things useful in determining the final height is the initial vertical speed and the deceleration in that direction.
Using the second method we find that the block has a vertical velocity of 5m/s which when used to calculate Kinetic Energy (0.5 m v^2) effectively tells us the energy that would be converted to gravitational potential energy if no other forces were acting (as is the case here). I'm not saying that energy is a vector quantity but simply that the kinetic energy calculated here is the energy that could be transformed into gravitational potential if the block was 'bound' to a frictionless edge. In this case the 'involved kinetic energy' is only 12.5J and so gh=12.5, h is approx 1.3m.
Using the first method we can resolve the force of gravity acting along the slope (and opposing the blocks movement) to be 19.62N. Using expressions for energy 19.62*h=50J, h is approx 1.3m. Using equation of motion: s=u^2/2a (as v=0) and so s= 2.548 (approx), this is the slope length travelled, so through further resolution, the vertical height travelled is once again about 1.3m.
I think it is important to remember the direction in which a force is acting, if you could simply equate a velocity in a direction that is not parallel to the force causing a deceleration to an energy then there is no reason why an object travelling horizontally on a frictionless surface wouldn't slow down (the force would still be acting and now direction doesn't matter so we could just apply E=Fd to find that there is a horizontal deceleration). There would also be no reason (other than through common sense) not to take the block moving with a projectile motion initially, as you would be applying a downwards force that is not-restricted through the wedge surface on the block. If you view it this way and use the equation, s(height)=[u^2*sin(theta)^2]/2g then you again get the height is approximate to 1.3m.
I am not disagreeing with you working of the projectile motion, but disagree that it even reaches the end of the wedge in the first place. Your mistake (I think) was in you suggesting that mgh could be used without resolving the force. If this were the case then the above abnormalities would seem to occur.
P.S. If this is all wrong, then can you please explain why?
Also, I am assuming an initial velocity of 10m/s and NOT a velocity of 10m/s along the entire incline, but obviously if this was not the case then the above is not valid.
Log in to reply
You made a mistake. What Ritesh Yadav did is correct.
Kinetic Energy is a scalar quantity. The v in 2 1 m v 2 doesn't care which way your velocity is pointing. That's the whole allure of the energy approach—we can ignore direction and just do our calculations solely using scalars and still get the right answer.
Let's think about the block. It's on a wedge which doesn't move throughout the scenario. You correctly said that gravity is acting on the object. What you missed is the fact that the wedge is also exerting a normal force perpendicular to the its surface. When we resolve this along the x − and y − directions, you'll find that the acceleration in the y -direction isn't exactly g . Moreover, you'll find that the block's velocity's x -component changes too.
This makes sense. Think about it. The block's velocity's x -component has to proportionally change with the y − component. Otherwise, the angle that the velocity makes with the x − axis won't be 30 degrees and the block will either start flying before it reaches the end of the wedge or go through the wedge—both of which are nonsensical scenarios.
Let's do the calculation your way, taking the normal force exerted by the wedge on the block into account. (Just note that in the wild, one would be heavily discouraged from trying to do it this way since it's so calculation-intensive and unnecessary.)
The net force in the y -direction, F y , is − m g + N cos θ where g is the acceleration due to gravity, N is the normal force, and θ is the angle that the wedge makes with the horizontal, which is 30 degrees. (I'm taking the downward direction as negative.)
Similarly, the net force in the x − direction is F x = − N sin θ .
We know that N = m g cos θ , which means that a y = − g ( 1 − cos 2 θ ) = − g sin 2 θ = − 4 1 g and that a x = − g sin θ cos θ = − 4 3 g
(For the problem, we take g = 1 0 m ⋅ s − 2 .)
If we use these values in the equation v 2 = u 2 + 2 a s (note that a and s need to be in the same direction), then we get v y / top = 5 2 − 2 ( 4 1 g ) ( 1 . 8 ) = 4 m ⋅ s − 2 and v x / top = ( 5 3 ) 2 − 2 ( 4 3 g ) ( 1 . 8 cot θ ) = 4 3 m ⋅ s − 2 where v y / top is the y − component of the block at the top of the wedge and v x / top is the x − component of the block at the top of the wedge.
Strictly speaking, we don't need v x / top to do the problem. However, note that the angle made by the block's velocity with the horizontal is still tan − 1 ( 4 3 4 ) = 3 0 ∘ , exactly as we would expect.
Now that we have v y / top , we can use the equation v 2 = u 2 + 2 a s once again to find the extra height traveled: 0 = 1 6 − 2 ( 1 0 ) h ⟹ h = 0 . 8 m
Hence, the height attained by the block is H + h = 2 . 6 m .
TL;DR: You forgot to take the normal force into account.
Problem says "...given a velocity of 10m/s along the incline". Gave me the impression that the velocity is maintained at 10m/s troughout its travel along the incline.
The question says the block lies on an inclined plane. So what i did was, I took the components along x and y direction, but couldn't proceed. Can u help me with this?
That's annoying, I got the same answer you did but it considered my answer wrong because I included three significant figures and gave the "correct" answer as 2.6.
The block will cover 3.6 m along the inclined with a decelration of 5 m/s^2 in the direction opposite to the motion.Just reaching the edge of the wedge it will have a velocity of 8 m/s at an angle of 30 degree with thw horizontal. Then it will behave like a projectile and h max can be easily calculated using v^2-u^2 =2as
The block will follow the projectile motion after leaving the wedge. Find the velocity of block when it leaves the wedge by v^2-u^2=2as. Here a will be -gsin(30) Now find the height of the projectile by v^2 sin^(30)/2g(=h) Now add 1.8 and h. You will get the answer. :)
Why don't simply use work-energy theorem and then add the initail height? only force is mg therefore using mgh=1/2m[(final velocity)^2-100]
Log in to reply
You can do so. It is just slightly different approach to the same question. :)
First calculate the motion of the block on the wedge. Find the weight of the object or the force of gravity (note: acceleration due to gravity = − 1 0 m / s 2 ):
F = m a s s × a c c e l e r a t i o n
F = 1 k g × − 1 0 m / s 2
F = − 1 0 N
Find the component of the gravity force that affects the block on the wedge (an explanation of this formula can be found here ):
sin 3 0 ∘ × − 1 0 N = − 5 N
The acceleration of the block on the inclined plane is then − 5 m / s 2 because a c c e l e r a t i o n = m F = 1 k g − 5 N
Find the length of the inclined plane:
1 . 8 m / sin 3 0 ∘ = 3 . 6 m
Now that we know the distance along the incline, the acceleration due to gravity along the incline, and the initial velocity along the incline, we can calculate the velocity at the moment the block reaches the end of the wedge and begins projectile motion:
( V f ) 2 = ( V i ) 2 + 2 × a × d
( V f ) 2 = ( 1 0 m / s ) 2 + 2 × − 5 m / s 2 × 3 . 6 m
V f = 8 m / s @ 3 0 ∘
Now the projectile motion part. Find the vertical component of the velocity because we are only dealing with vertical position:
sin 3 0 ∘ × 8 m / s = 4 m / s
The height of the projectile relative to where it was launched is:
h e i g h t = V i ⋅ t + 2 1 ⋅ g ⋅ t 2
h e i g h t = 4 m / s ⋅ t + 2 1 ⋅ − 9 . 8 m / s 2 ⋅ t 2
The max height is the vertex of this quadratic equation and can be found using several methods. You then have to add 1.8 m to the max height because the projectile was launched from 1.8 m.
This is the method I used:
I found the two roots by setting height = 0 then solving for t.
0 m = 4 m / s ⋅ t + 2 1 ⋅ − 9 . 8 m / s 2 ⋅ t 2
t = 0 . 8 1 6 3 2 6 5 3 0 6 1 s e c and 0 s e c
The vertex is exactly half-way between the two roots.
t = 0 . 4 0 8 1 6 3 2 6 5 3
When you find the half-way point enter that value (t) into the equation and solve for height.
h e i g h t = 4 m / s ⋅ 0 . 4 0 8 1 6 3 2 6 5 3 s + 2 1 ⋅ − 9 . 8 m / s 2 ⋅ ( 0 . 4 0 8 1 6 3 2 6 5 3 s ) 2
h e i g h t = 0 . 8 1 6 3 2 6 5 3 0 6 1 m
0 . 8 1 6 3 2 6 5 3 0 6 1 m + 1 . 8 m = 2 . 6 2 m
As the speed given to the block at the bottom is enough to clear the inclined plane. Therefore after path will be a projectile.
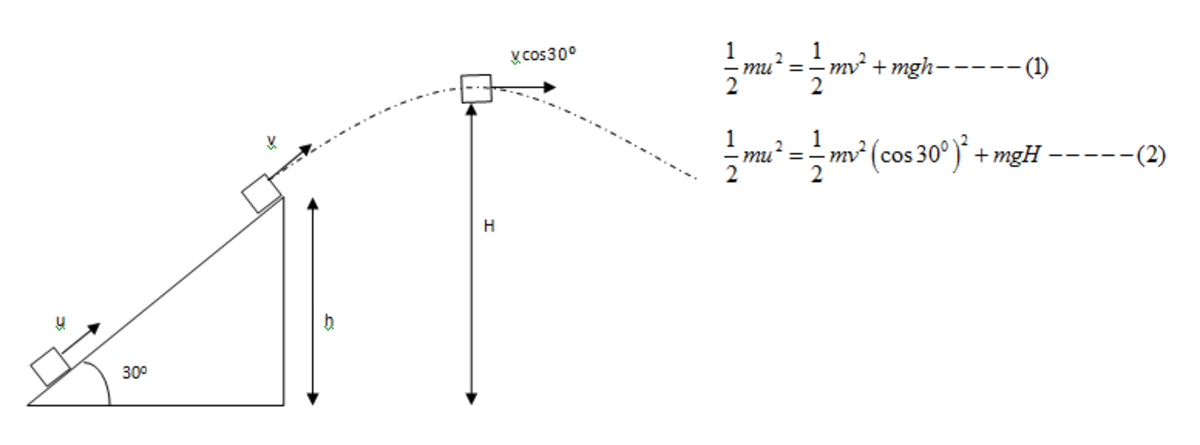
After solving the above two equations we will get H =2.6m
It can be seen in two steps. One for the time that it reaches the top of the wedge, and the other when it is like a projectile.
The time taken to reach top, that is cover 3.6m, is 0.4 seconds (s = ut + 1/2(a)t^2). At this point, velocity of block is 8 m/s. Now see this is a projectile. Max height is 0.8 m. Add this to the height of the wedge to get 2.6m.
Initial Kinetic Energy of the block = 50J
Kinetic energy on reaching the top of the slope i.e at 1.8 m
Height from the ground = 50 j - (1 x g x 1.8) { mgh lost }
= 32.36J
32.36 = 0.5m ( v e l o c i t y ) 2
v e l o c i t y 2 = 6 4 . 7 2
Now it will undergo projectile motion
Maximum height reached while projectile is
2 g u 2 ( sin θ ) 2
here initial angle of projectile is 30 degree
Height= 4 . 2 . ( 9 . 8 ) 6 4 . 7 2 = 0.82m
Hence total height covered = height covered on slope + height covered in projectile motion = 1 . 8 + 0 . 8 2 = ∗ ∗ 2 . 6 2 m ∗ ∗