You'll like to calculate it!

We can see $CM = BM$ . Now, the midpoint of hypotenuse is equidistant from all the 3 vertices of a right triangle. So $DM = BM = 3OM$ $\Rightarrow tan \angle ABC = \dfrac{OM}{3OM} = \dfrac{1}{3}$

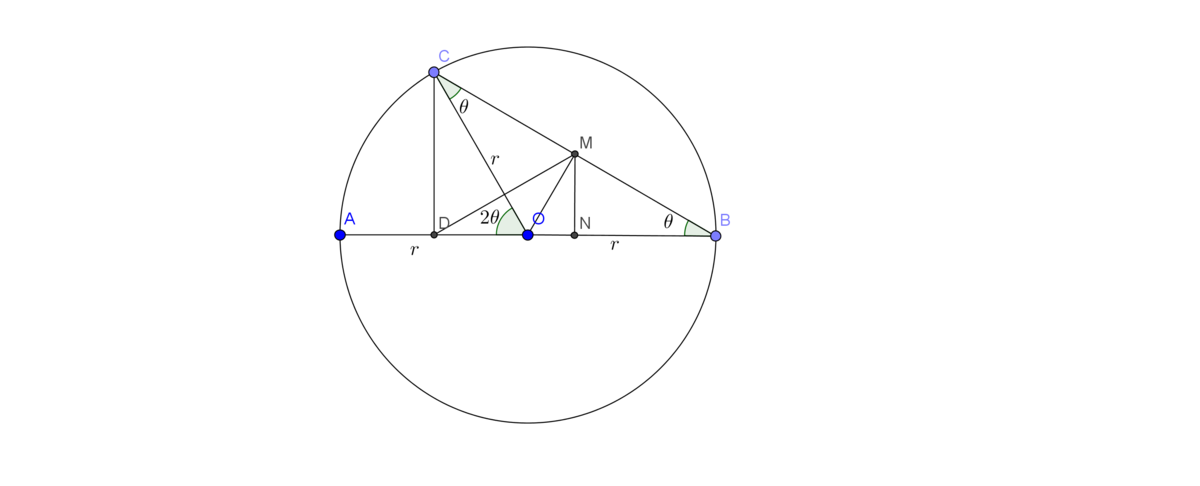
As $OM \perp BC$ , so $CM=BM, \angle OCB =\angle OBC$ .

Let radius $OC=OB=OA=r$ and $\angle ABC=\theta$ . Then, $\angle AOC = 2\theta$

Let's draw a line $MN$ perpendicular to $AB$ .

$CD=r \sin 2\theta, ~OD=r \cos 2\theta, ~ OM=r \sin \theta, ~DM=3r \sin \theta$ .

As, $\triangle BDC$ and $\triangle BNM$ are similar triangles and $BM=\frac{1}{2} BC$ , so $\begin{aligned} MN &=\frac{1}{2}CD \\ &=\frac{1}{2}r \sin 2\theta \\ &=r \sin\theta \cos\theta \end{aligned}$

Again, $\begin{aligned} ON^2 &= OM^2 -MN^2 \\ &=r^2 \sin^2 \theta - r^2 \sin^2 \theta \cos ^2 \theta \\ &=r^2 \sin^2 \theta (1- \cos^2\theta) \\ &=r^2 \sin^4 \theta \end{aligned}$ Hence, $ON=r \sin^2 \theta$

Again, $\begin{aligned} DM^2 &=DN^2+MN^2\\ &= (r \cos 2\theta+r \sin ^2 \theta)^2+r^2 \sin ^2 \theta \cos ^2 \theta \\ &=r^2 (1-2\sin^2 \theta +\sin ^2 \theta)^2 +r^2 \sin ^2 \theta \cos ^2 \theta \\ &=r^2 \cos^4 \theta +r^2 \sin ^2 \theta \cos ^2 \theta \\ &=r^2 cos^2 \theta (cos^2 \theta +\sin ^2 \theta)\\ &=r^2 cos^2 \theta\\ (3r\sin \theta)^2 &=r^2 cos^2 \theta\\ tan^2 \theta &=\frac{1}{9}\\ tan \theta &= \frac{1}{3} \end{aligned}$

The answer will be $1+3=4$

Let O be the origin and Q:(-a.b) and let the circle radius be R. Hence, B:(R,0), M:((R-a)/2,b/2) and D:(-a,0). We then have the following two equations: a²+b²=R² & 9OM²=DM² or(1/4)((R+a)²+b²)= (9/4)((R-a)²+b²). These can be easily solved to give, a=4R/5 & b=3R/5. Now tan(θ) = b/(a+R) =(3R/5)/((4R/5)+R)=1/3. Hence a+b=4