Your Friend’s Ratio “Mistake”
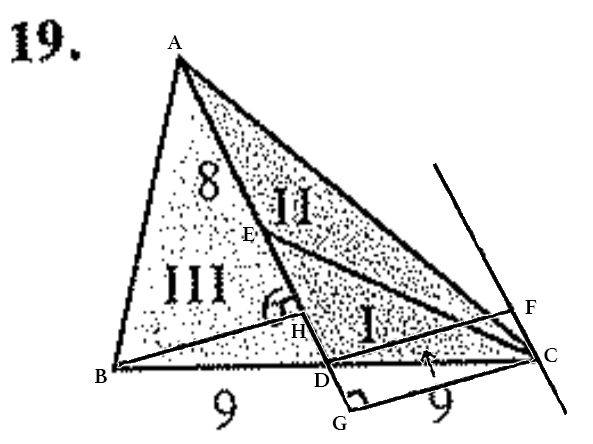
While you are reviewing the ratio of figures in geometry, one of your questions is to find the ratio of area I and area I I I for the problem below. While you are “supposed” to use the fact that area I I I = I + I I and that triangle I and I I share a height, one of your friends “mistakenly” just used two random known sides on triangle I and I I I , giving him 6 : ( 8 + 6 ) = 3 : 7 , which turned out to be the correct answer. Upon asking your teacher about why that worked she said that the numbers just “happened to work out that way”, but you aren’t completely sure if that is right.

Was your teacher correct that the method just happened to work out, and there is no direct reason for the connection?
Notes: For there to be a direct connection, this relationship must work for all situations like this, not just the situation in the diagram above.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Sorry for the confusion, my hope for the problem was that while yes, by using these two sides you arrive at the correct solution, is there a “ direct ” connection between using these two sides for any scenario like this? I’ve hopefully made the question more clear, thanks for the help!
Wow unused the same reasoning yet answered wrong... Better reading next time haha.
After me and my friend ran into this problem we tried using the ratio properties of triangles we had learned to understand why this result happened. When two triangles share a height, the ratio of their areas is the same as the ratio of their bases. Therefore, we tried finding a way to prove that the altitude of △ C E D (in the diagram below) drawn to A G is congruent to the altitude of △ A B D drawn to A G .
Finally before we make some real headway into the problem, we should formalize what we are even trying to prove, which is,
For any △ A B C , let A D be the median drawn from point A to B C . Let E be any point on A D . The ratio of the areas △ A B D and △ C E D is equal to the ratio of A D to E D .
 Triangle Diagram
Triangle Diagram
To prove this lets start by drawing altitudes B H and C G to their respective bases. To make it easier to visualize what's about to happen, lets move C G "up" along its base, keeping it perpendicular to B G , giving us D F (note that it's length remains the same as it forms a rectangle). Because B H and D F are both perpendicular to the same line ( A G ), B H ∥ D F . Base B C is a transversal that cuts B H and D F , so ∠ H B D ≅ ∠ F D C , and because of the A A S Congruency Theorem, △ B H D ≅ △ D F C . Then, the altitudes are congruent, so the ratio of areas is equal to the ratio of bases, and we've proved our conjecture.
It turns out that there is a reason for the relationship and the numbers didn't just happen to work out, pretty neat!
I'm not sure I understood the point here as the answer seems to be given in the question. Nevertheless....
We use the notation A I for the area of triangle I , etc. As noted in the question, A I I I = A I I + A I , because the triangle formed by combining triangles I I and I has an equal base and the same height as triangle I I I . Also as noted, triangles I and I I have equal heights; but this means that the ratio of their areas will equal the ratio of their bases. So A I : A I I = 6 : 8 ⟹ A I : A I I + A I = 6 : ( 8 + 6 ) = 3 : 7 [and then, because A I I I = A I I + A I ] ⟹ A I : A I I I = 3 : 7