You're getting very sleeping cause I'm pulling the string very slowly
A pendulum consists of a point-mass object of mass suspended from a pivot by a massless string of length . The pendulum is swinging freely in the vertical plane. By what factor does the amplitude of oscillation change if the string is very slowly shortened by a factor of ?
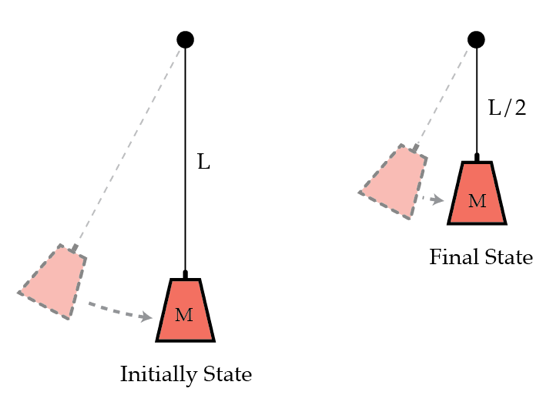
Details and assumptions
The amplitude of oscillation is very small.
The answer is 1.68.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The average tension of the string (with m as the mass of the object, L as the length of the pendulum, g as the gravitational constant and θ o as the angular amplitude of oscillation) is:
T = m g cos θ + m L θ ˙ 2 = m g ( 1 − θ 2 ) + m L θ ˙ 2 = m g ( 1 + 4 θ o 2 )
Use that θ ( t ) = θ o cos ( l g t + ϕ ) . The oscillation energy and potential energy is E = − m g L cos θ o ≈ − m g L ( 1 − 2 θ o 2 ) , and we balance the work done by shorten the pendulum length with the change in the oscillation energy to get:
d E = − m g d L + 2 1 m g θ o 2 d L + m g L θ o d θ o = d A = − T d L = − m g ( 1 + 4 θ o 2 ) d L ⇒ L d θ o = − 4 3 θ o d L
⇒ θ o ∼ L − 3 / 4
So the change in the amplitude must be k 3 / 4 = 1 . 6 8