This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
You could just write 1 0 instead of " r = 1 0 ". Bonus question: Can you prove that 1 3 + 2 3 + … + n 3 = ( 2 n ( n + 1 ) ) 2 by telescoping sum?
Let's prove k = 1 ∑ n k 3 = ( 2 n ( n + 1 ) ) 2 using induction!
Let's establish our base case n = 1 . Clearly, k = 1 ∑ 1 k 3 = ( 2 1 ( 1 + 1 ) ) 2 = 1 .
Now, onto the induction hypothesis. First, we assume k = 1 ∑ n k 3 = ( 2 n ( n + 1 ) ) 2 for some n . Then, since
k = 1 ∑ n + 1 k 3 = ( n + 1 ) 3 + ( 2 n ( n + 1 ) ) 2 = 4 n 2 ( n + 1 ) 2 + 4 ( n + 1 ) 3
= 4 ( n + 1 ) 2 ( n 2 + 4 ( n + 1 ) ) = ( 4 ( n + 1 ) ( n + 2 ) ) 2
Thus, our hypothesis is proven and our induction is complete!
Log in to reply
Nicely done, but I prefer telescoping sum rather than induction.
Nice work. Easier then the way I solved it that's for sure.
Starting, by first looking at 1x1x1, the square root will be 1, then if we add 2x2x2 that will gives us 9 or a square root of 3, and if we add 3x3x3 to that will give us 36 or a square root of 6. Next if we add 4x4x4 one more time, that will give us 100 or a square root of 10. Lastly, if we look at the connection between 1, 3, 6, 10 they are the consecutive triangular numbers. Therefore, the last sum is 10x10x10 so the tenth triangular number is 55 (you can check using Pascal's Triangle or the triangular number formula). So the square root of everything under the radical is 55.
Please upvote if you liked this solution.
The sum of the cubes of the first n integers is the square of the sum of the first n integers. So the square root of the sum of the first 10 cubes is the sum of the first 10 integers.
1+2+3+...+10 = 10(10+1)/2
= 110/2
= 55
Moderator note:
Can you explain why your first line works?
Great! (y)
yes I assumed its true because its a standard formula
Consider 1+2+3+4+...+n. Arithmetic sequence, first term 1, number of terms n, common difference 1.
So Sn = (n/2)(2x1+1(n-1))
Sn = n(n+1)/2
So 1+2+3+4+...+n = n(n+1)/2
Consider 1^3+2^3+3^3+...+n^3
Using induction its easy show that this is equal to 0.25(n^2)(n+1)^2. Just prove its true for n=1 but substituting n=1 into both sides, then assume true for n=k, then prove it for n=k+1 by adding (k+1)^3 to 0.25(k^2)(k+1)^2, then make the bases of the 2 fractions of the same and factorising out the (k+1)^2. Then you will have the initial statement for n=k+1.
0.25(n^2)(n+1)^2 = ((n(n+1)/2))^2.
So 0.25(n^2)(n+1)^2 = (1+2+3+4+...+n)^2.
So 1^3+2^3+3^3+...+n^3 = (1+2+3+4+...+n)^2.
As this question also has cube of 1 i.e 1^3+2^3......
So we can simply multiply last digit i.e 10 to its next number that will divide the answer by 2
we get 10×11=110/2= 55 ans.
Moderator note:
This solution is basically going through the labor of calculating all the terms. It is correct but impractical. For a simpler approach, see Abhishek Sharma's solution.
there was no need to find 3025 as u first squared 55 and then found the root
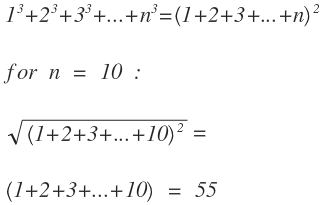
r = 0 ∑ 1 0 r 3
Using the formula r = 1 ∑ n r 3 = ( 2 n × ( n + 1 ) ) 2 we have,
( 2 1 0 × ( 1 0 + 1 ) ) 2 ( 2 1 0 × ( 1 0 + 1 ) ) 5 5