Yummy Jelly
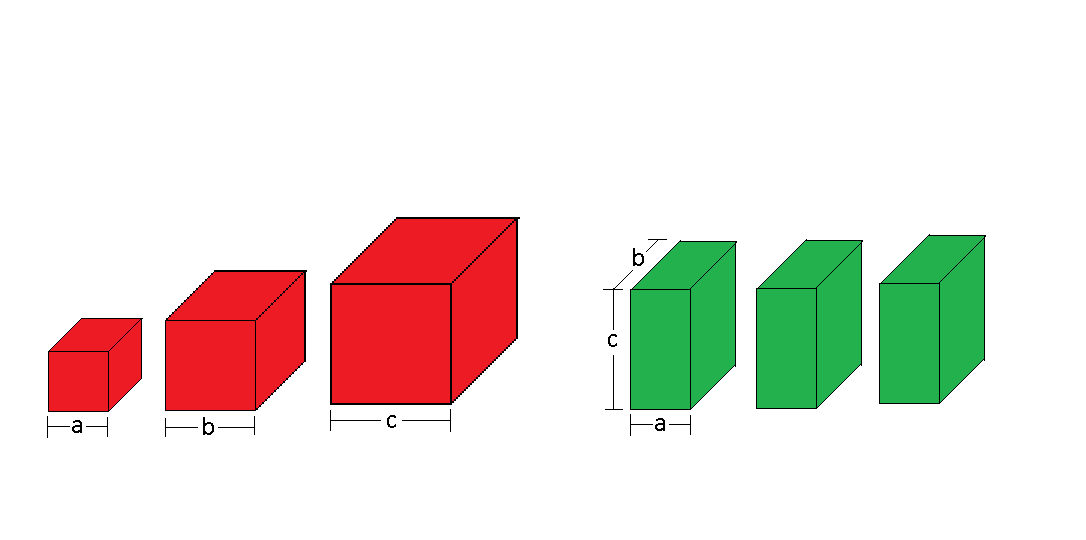
A jelly shop sells its products in two different sets: 3 red jelly cubes and 3 green jelly cuboids.
The 3 red cubes are of side lengths a < b < c , while the 3 green cuboids are identical with dimensions a × b × c , as shown above.
Which option would give you more jelly?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Simple standard approach.
Interesting approach, Dr. Warm. I solved it in a slightly different way. We know that a 3 + b 3 + c 3 − 3 a b c = 2 1 ( a + b + c ) ( ( a − b ) 2 + ( b − c ) 2 + ( c − a ) 2 )
We see that the RHS is positive since a , b , c are not all equal. Hence the volume of red jellies is (strictly) greater than the volume of the green jellies.
I did it the same way
We know that AM GM inequality could be proved using Cauchy Induction ( or the Forward Backward induction) but can this approach to induction be applied to the other formulae that we can prove with induction ( weak and strong) or it has no other applications.If the former is true I would like to know how?
Sum of the volumes of the three red cubes= a 3 + b 3 + c 3
sum of volumes of the three green cuboids= abc + abc + abc= 3abc
AM >= GM
( a 3 + b 3 + c 3 )/3 >= cube root ( a 3 b 3 c 3 )
a 3 + b 3 + c 3 >= 3abc
a>b>c so equality is not possible because for equality, a=b=c
therefore a 3 + b 3 + c 3 > 3abc
hence, volume of the three cubes > volume of the three cuboids
From the given information, obviously the volume of the red jelly = a 3 + b 3 + c 3 .
On the other hand, the volume of the green jelly = 3 a b c .
According to Arithmetric Mean - Geometric Mean Inequality , 3 a 3 + b 3 + c 3 ≥ 3 a 3 b 3 c 3 = a b c .
Hence, a 3 + b 3 + c 3 ≥ 3 a b c .
Since the inequality will become equation if and only if a = b = c , the volumes of both jelly sets can never be equal.
As a result, the red jelly will have more volume than the green one.