Yummy Straight Lines
 y
=
2
x
is the angle bisector of the lines
y
=
x
and which of the following lines?
y
=
2
x
is the angle bisector of the lines
y
=
x
and which of the following lines?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Alternately, One could consider that
c o s ( θ ) = ∣ u ∣ ∣ v ∣ u ⋅ v .
A point for y=x is (1,1), for y=2x is (1,2), and for y=mx is (1,m).
The angle between y=x and y=2x is the same as between y=2x and y=mx.
So the cosines would be the same.
c o s ( θ ) = 2 5 3 = 5 1 + m 2 1 + 2 m
Simplifying, this reduces to the quadratic
m 2 − 8 m + 7 = 0 o r m = 7 , m = 1
Great analysis, Stuart. :)
@Rajen Kapur Nice problem. I was surprised that the solution line had an integer slope.
nice..!!!!
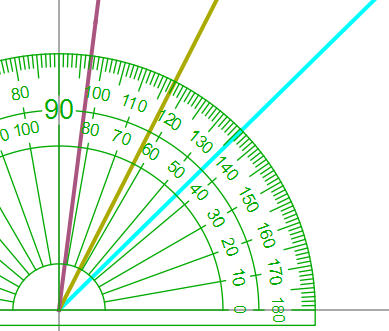
The line y = x makes an inclination of 45 degrees with x axis.
The line y = 2x makes an inclination of Arctan(2) with x axis which is equal to ~ 63.435 degrees.
The angle between y=2x and y=x is 18.435 degrees.
If the line y = 2x is angular bisector of y= x and y = mx ,then y=mx should make an inclination of (63.435 + 18.435) degrees with x-axis.
Therefore m should be equal to tan(63.435 + 18.435) or 7
Therefore y= 2x is angular bisector of y=x and y=7x.

The line y = x forms angle θ 1 = 4 π with the positive x axis. Let θ 2 denote the angle between y = x and y = 2 x . Denote the line we are to find by L 3 : y = m x and let θ 3 denote the angle between L 3 and the positive x axis.
We have θ 2 = arctan 2 − 4 π and thus θ 3 = 2 arctan 2 − 4 π .
Therefore m = tan θ 3 = 1 + tan ( 2 arctan 2 ) tan ( 2 arctan 2 ) − 1
⇒ m = 1 + 1 − 4 4 1 − 4 4 − 1 = 7 .
Alternatively, we can approach the whole problem from a vectors points of view:
Consider the reflection of the point with position vector p = ( 1 1 ) in the line r = λ ( 1 2 ) . Denote by q the position vector of the point on the line closest to p . We have ( 1 2 ) ⋅ ( λ − 1 2 λ − 1 ) = 0 from which we deduce λ = 0 . 6 . That is, q = ( 0 . 6 1 . 2 ) .
Thus the image of p after reflection is ( 1 1 ) + 2 ( − 0 . 4 0 . 2 ) = ( 0 . 2 1 . 4 ) .
Therefore, since the origin is invariant under this transformation, the image line has equation y = 7 x .