Z Virus

Relevant wiki: Bayesian Theory in Science and Math

According to Bayes' Theorem , $P(A \mid B) = \frac{P(B \mid A)} {P(B)} P(A). \ _\square$ for events $A$ & $B$ .

Let $A$ be the event of true zombie patient and $B$ be the event of positive test.

Then we already know that the sensitivity (positive if zombie) = $P(B \mid A)$ = 90%.

And $P(A)$ = 10%.

All we need to know is $P(B)$ to evaluate the desired $P(A \mid B)$ .

Since the positive results may involve true positive (called $B+$ ) or false positive (called $B-$ ), we can combine these independent probability as followed ( $-A$ is non-infected event.):

$P(B+) = (P(B \mid A) (P(A)$ ) = (90%)(10%) = 9%

$P(B-) = (P(B \mid -A) (P(-A)$ ) = (100% - 70%)(90%) = 27%.

$P(B) = P(B+) + P(B-)$ = 36%.

Hence, $P(A \mid B) = \dfrac{9}{36} = \dfrac{1}{4}$

Thus, $a+b = 5$ .

let $A$ = person is a zombie

let $B$ = test result was true

We want $P(A|B) = \frac{P(B|A)}{P(B)} \times P(A)$

$P(B|A) =$ "test result was true for an actual zombie" $= \frac{9}{10} =$ 90%, as given in the question.

$P(B)$ = "got a true test result". The test returns true 90% of the time for actual zombies, and 30% (false positives) of the time for non-zombies. $\frac{1}{10}$ th of the population are zombies and $\frac{9}{10}$ ths are non-zombies, so: $P(B) = (\frac{9}{10}\times\frac{1}{10}) + (\frac{3}{10}\times\frac{9}{10}) = \frac{36}{100} = \frac{9}{25}$

$P(A) = \frac{1}{10}$ as given in question.

So, $P(A|B) = \frac{\frac{9}{10}}{\frac{9}{25}}\times\frac{1}{10} = \frac{25}{100} = \frac{1}{4}$ .

$1+4 = 5$ .

The problem can be solved without actually applying Bayes' Theorem though one might argue that it's the same in the end. This is just an other perspective into the problem. The problem can be broken down into a simple probability equation, P(E) = $\frac{A}{B}$ , where A is the number of required outcomes of the event E and B is the total number of possible outcomes of an event E.

In this case, A is the true number of zombies according to the test being positive. B is the total number of zombies according to the test being positive.

In the question it is given that test kit is 90% sensitivity meaning for every 100 actually infected people, the test will show only 90 peoples' result as positive. 70% specificity meaning, out of every 100 non infected people, 30 peoples' result will be shown as positive.

Let the total population of the world be 100, this would mean that 10 are actually infected.Thus, 90 are not infected.

So B would be (number of actually infected)(percentage of them being positive after the test) + (number of non-infected people )(percentage of them being positive after the test), B = 10x0.9 + 90x0.3 = 36 and A would be (number of actually infected)(percentage of them being positive after the test) = 10x0.9 = 9

So we have the answer as P(E) = $\frac{A}{B}$ = $\frac{9}{36}$ =0.25

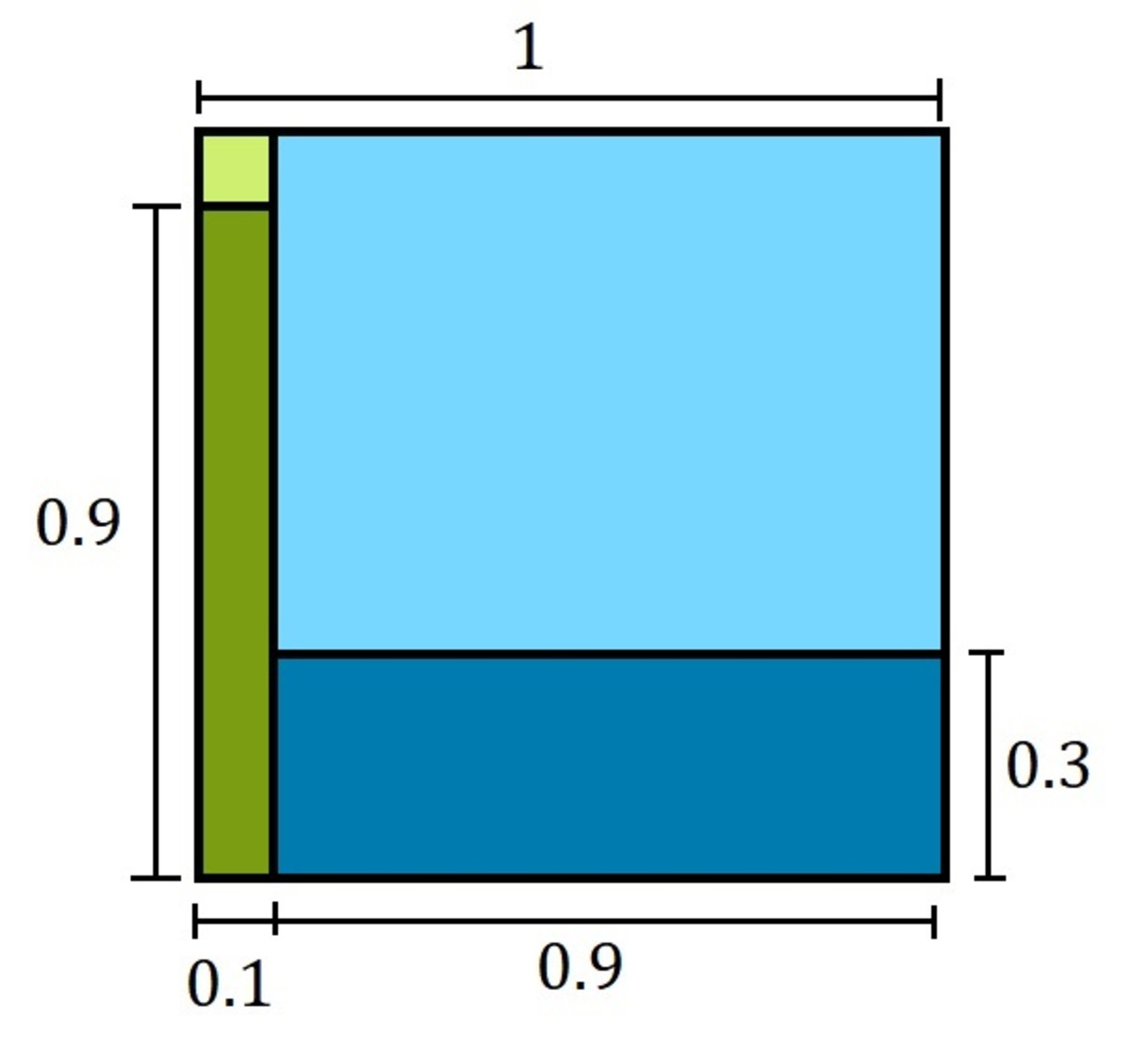
I want to provide a visual explanation for this problem. In the diagram above we have a square with side length $1$ . This square represents the whole population. The $\color{#20A900}\text{green}$ part of this diagram (light and dark green) represents the amount of people that are infected. The area of this region is $0.1$ because 10% of people are infected. The $\color{#3D99F6}\text{blue}$ part of this diagram (light and dark blue) represents the amount of people that are not infected. The area of this region is $0.9$ because 90% of people are not infected.

Notice we have light and dark regions.

The light green region represents the amount of infected people we expect to test negative. The area of this region is $0.01$ because from the 10% of people are infected we expect the test to fail 10% of the time.

The dark green region represents the amount of infected people we expect to test positive. The area of this region is $0.09$ because from the 10% of people are not infected we expect the test have a success 90% of the time.

The light blue region represents the amount of not infected people we expect to test negative. The area of this region is $0.63$ because from the 90% of people are not infected we expect the test to have a success 70% of the time.

The dark blue region represents the amount of not infected people we expect to test positive. The area of this region is $0.27$ because from the 90% of people are not infected we expect the test to fail 30% of the time.

Here we are interested in the darker regions. These regions contains all people we expect to test positive. This whole region has an area of $0.36$ . Inside this region we can find the people who are infected and the people who are not infected. The dark green region is the region where all infected people test positive.

It means that the probability of a person being infected given that the test was positive will be $\frac{0.09}{0.036}=\frac{1}{4}$ . The answer for the problem will be $1+4=\boxed{5}$ .

Think for a moment about what exactly the diagram tells. When we say "the probability of being infected given the test was positive" means we should shrink our sample in order to fit the conditions. The condition says that the test was positive. What we do is to look only for the people we expect to test positive. Inside this group we will find infected and not infected people. We just need to know the proportion and it is done!

Let Z = Event that person has the Z-virus. P(Z) = 0.1

Z' is the complement of Z.

P = Event that person is tested positive.

P' is the complement of P.

P (P|Z) = P (P ∩ Z) / P(Z) = P (P ∩ Z) / 0.1 = 0.9

P (P|Z') = P (P ∩ Z') / P(Z') = P (P ∩ Z') / 0.9 = 0.3

=> P(P) = 0.9 * 0.1 + 0.3 * 0.9 = 0.9 + 0.27 = 0.36

The probability that the tested subject was truly zombie given that they had a positive result:

P (Z|P) = P (P ∩ Z) / P(P) = (0.9 * 0.1) / 0.36 = 1 / 4

I found a tree diagram helpful in visualising this.