Zebra For Lunch

Calculus Level 3

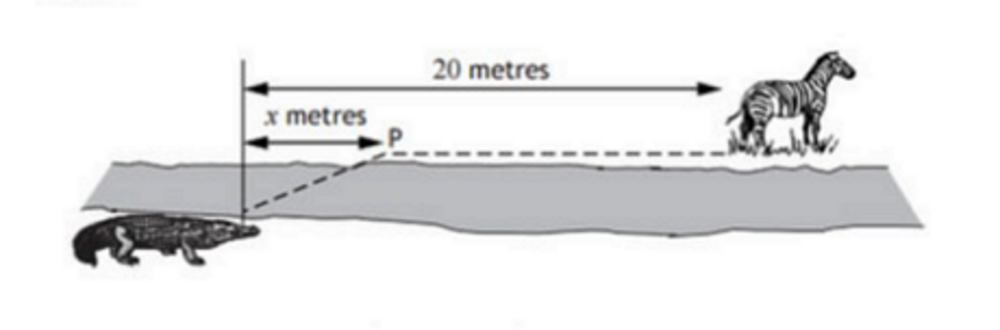
A crocodile is stalking a prey located 20 metres further upstream on the opposite bank of a river. It can travel at different speeds on land and in water. The time taken for the crocodile to reach its prey can be minimized if it swims to a particular point, $P$ , $x$ metres upstream on the other side of the river as shown in the diagram above. Let the time taken, $T$ , measured in tenths of a second, be given by

$T(x) = 5\sqrt{36+x^2} + 4(20-x)$

Considering the times $T$ where $x= 0$ and $x =20$ , there is a value of $x$ between 0 and 20 which minimizes $T$ . If $x=a$ is the point at which $T(a)$ is minimized, find the value of $a + T(a)$ .

The answer is 106.

2 solutions

Muhammad Arifur Rahman
Oct 24, 2015

You can make it with some programming. Here's the one with C++

#include <stdio.h>
#include <math.h>
int main()
{

double tx,ta=500,x=0,a;
while(x<=20){
tx=(5*sqrt(36+pow(x,2)))+(4*(20-x));
if(tx<ta)
{
ta=tx;
a=x;
}
printf("For x=%.0lf, Time=%.5lf\n",x,tx);
x++;
}
printf("\nAs at x=8, Time is minimum,\n\n\t\ta=%.0lf\n\tT(a)=%.5lf\n So,\n\n\t\ta+T(a)=%.0lf",a,ta,a+ta);
printf("\n\n");
return 0;
}

Chew-Seong Cheong
Sep 18, 2019

$\begin{aligned} T(x) & = 5\sqrt{36+x^2} + 4(20-x) \\ \frac {dT}{dx} & = \frac {5x}{\sqrt{36+x^2}} - 4 & \small \color{#3D99F6} \text{Putting }\frac {dT}{dx} = 0 \\ 5x & = 4\sqrt{36 + x^2} & \small \color{#3D99F6} \text{Squaring both sides} \\ 25x^2 & = 16\times 36 + 16 x^2 \\ 9x^2 & = 16\times 36 \\ \implies x & = 8 \end{aligned}$

Since $\dfrac {d^2T}{dx^2} = \dfrac 5{\sqrt{36+x^2}} - \dfrac {15x}{2(36+x^2)^\frac 32} > 0$ when $x = 8$ , $\implies \min(T(x)) = T(8) = 5\sqrt{36+8^2} + 4(20-8) = 98$ , $a=8$ , and $a+T(a) = 8 + 98 = \boxed{106}$ .

Zebra For Lunch

The answer is 106.

2 solutions

0 pending reports