Zig-Zag
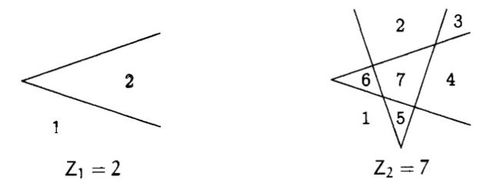 Let us say that
Z
n
is the maximum number of regions which can be determined by
n
lines containing exactly one sharp turn (see image of
Z
1
and
Z
2
for examples).
Let us say that
Z
n
is the maximum number of regions which can be determined by
n
lines containing exactly one sharp turn (see image of
Z
1
and
Z
2
for examples).
Find Z 1 0 0 .
The answer is 19901.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The general expression is nC2+1 where n is number of 'straight' lines 2 0 0 C 2 + 1 = 1 9 9 0 1
first lets look at Z 1 , 2 lines divide the space into 2 regions: inner and outer. (2C2+1=2) but this doesn't explain it all.
So lets look at Z 2 , now if we select any 2 lines from 4 [4C2] we will get a unique inner region corresponding to each. (regions 2,3,4,5,6,7) also one outer region will be mutual to all (region 1) So the solution becomes 4C2+1=7
for Z 1 0 0 , we will be selecting 2 lines from 200 lines for corresponding inner region (200C2) and one mutual outer region. 200C2+1=19901
NOTE: If there is a confusion that when we select the 2 lines (those equivalent to 2 lines in Z 1 ) 3 regions are formed (6,7,4) then consider it this way, those 2 lines form only region 6. region 4 will be formed when we select the "vertical right" line and "horizontal lower" line. Similarly, region 3 will be formed when we select the "vertical right" line and "horizontal upper" line, region 7 by "vertical left" line and "horizontal lower" line, region 2 by "vertical left" line and "horizontal upper" line, region 5 by 2 vertical lines.
And here is my purely intuitive (but correct) guess: In problems like this, the number of extra regions (or intersections, etc.) created in each step tends to be a linear function of the number of lines present.
We already have Z 1 = 2 and Z 2 = 7 , and a quick sketch showed me that Z 3 = 1 6 . Thus the increment is Δ Z 1 , 2 = 5 and Δ Z 2 , 3 = 9 . Thus I assumed that the increments form an arithmetic progression with step size 4: Δ Z 1 , 2 , Δ Z 2 , 3 , … , Δ Z 9 9 , 1 0 0 = 5 , 9 , … , 3 9 7 ( = 5 + 9 8 ⋅ 4 ) . (The progression is confirmed by the fact that Δ Z 0 = 1 so that Δ Z 0 , 1 = 1 .)
To find the final number of regions, we must add all these increments to the initial value Z 1 = 2 . Note that the average value of the 99 increments is ( 5 + 3 9 7 ) / 2 = 2 0 1 , so that the answer is 2 + 9 9 ⋅ 2 0 1 = 1 9 9 0 1 . Note: since the increments Δ Z n , n + 1 are a linear function of n , the number of regions is a quadratic function of n . It is not difficult to see that Z n = 2 n 2 − n + 1 .