0=1 due to a polygon?

For any $n$ sided regular polygon inscribed in a circle of radius $r$, our objective is to calculate the perimeter of the polygon.

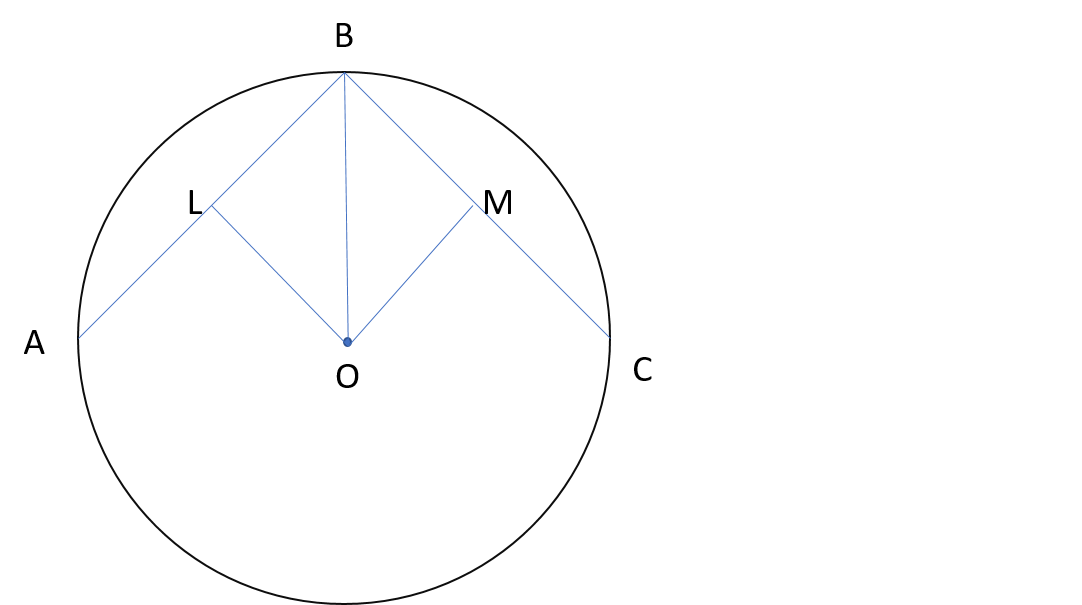
The figure represents the given situation. $O$ is the center of the circle and $AB$,$BC$ are edges of a regular polygon. $OL$ and $OM$ are perpendiculars drawn on line segments $AB$ and $BC$ respectively. Since perpendiculars from center bisect the chord, thus we have,

$OL = OM$

$OB = OB$

$\angle OLB = \angle OMB$

Therfore by RHS Criteration of congruency, $\Delta OLB \cong \Delta OMB$.

Thus by CPCT, we have

$\angle LBO = \angle OBM$

For any regular polygon of $n$ sides, each angle is given by $\frac{180(n-2)}{n}$.

Therefore, $\angle LBM = \frac{180(n-2)}{n}$. Thus $\angle LBO = \frac{180(n-2)}{2n}$.

Clearly,

$\frac{BL}{r} = cos(\frac{90(n-2)}{n}°)$

$\ BL = rcos(\frac{90(n-2)}{n}°)$ and thus,

$BC = 2BL = 2rcos(\frac{90(n-2)}{n}°)$

Since it is a regular polygon,

Perimeter = $(n)(BA) = 2nrcos(\frac{90(n-2)}{n}°)$ $.........................(1)$

But as $n$ approaches infinity the polygon tends to coincide the circle in which it is inscribed. Thus in that case the perimeter of the polygon becomes equal to the circumference of the circle in which it is inscribed.

Also As $n$ approaches infinity,

$cos(\frac{90(n-2)}{n}°)$ becomes approximately $cos(90°) = 0$ $.........................(2)$.

Also comparing the formula we obtained in equation 1 , to the circumference of circle,

$ncos(\frac{90(n-2)}{n}°) = \pi$ $.........................(3)$

From (2) and (3),

$\pi = 0$

Dividing by $\pi$ on both sides we get,

$0 =1$

Find the mistake!