Equations
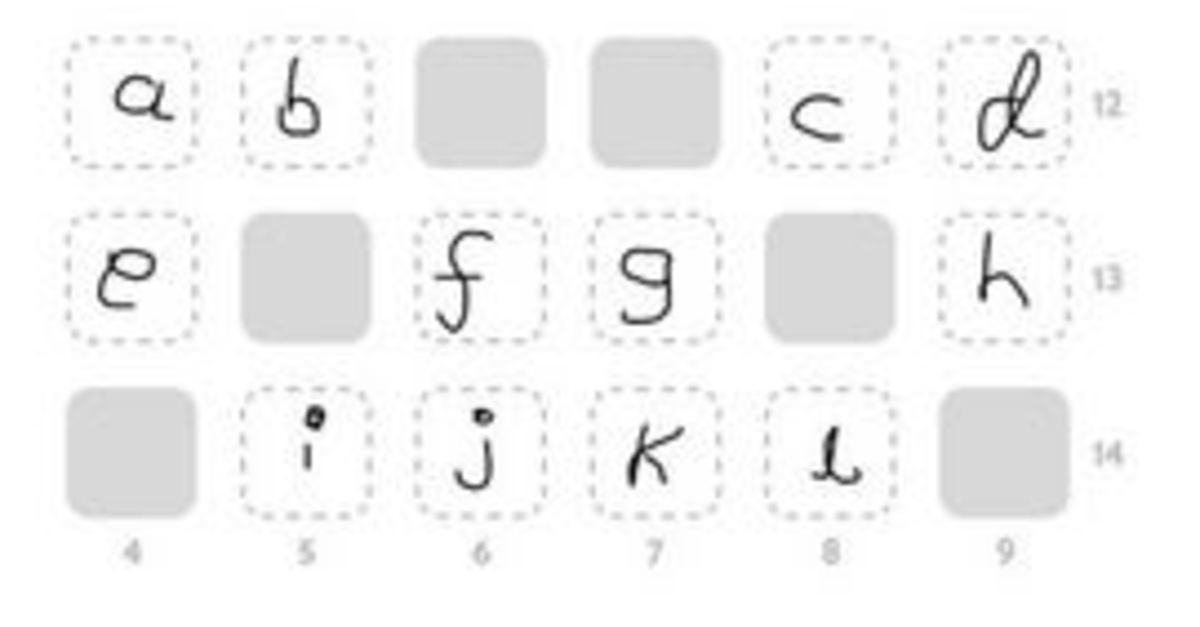
a+eb+if+jg+kc+ld+ha+b+c+de+f+g+hi+j+k+l=4=5=6=7=8=9=12=13=14
Brute-Force Case Work
a can be either one of 1,2 and 3.
d can be either one of 3,4,5 and 6.
Thus, their possible sums are 4,5,6,7,8 and 9.
b can be either one of 1,2,3 and 4.
c can be either one of 2,3,5 and 6.
Thus, their possible sums are 3,4,5,6,7,8,9 and 10.
(Let ∣ be the same as 'or'.)
So, a+b+c+d is the same as [4∣5∣6∣7∣8∣9]+[3∣4∣5∣6∣7∣8∣9∣10]
The only pairs here that make 12 are [3+9],[4+8],[5+7] and [6+6]
Meh, this is getting nowhere...
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
INCOMPLETE (and really frustrating...)
Haha bro, I hate problems like those. No point in solving them lol
Log in to reply
Yes...I abandoned this when I started getting hopeless lol
It turns out this problem is impossible. If the numbers from 1-10 are only allowed to be used ONCE, then we cannot solve column 1 or 2.
Comment if you want coding proof