2 Ways Of Calculating Probabilities & 2 Different Answers?

Hi All!

While reviewing probability, I stumbled upon what I thought was a routine problem:

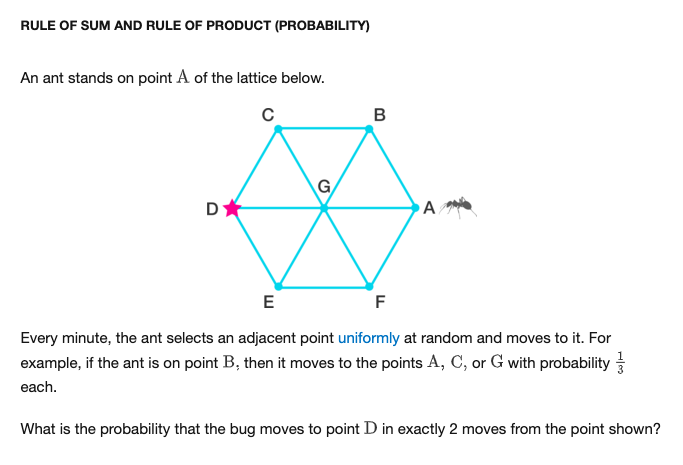
Mathematically, I would just multiply the # paths of the first step times the # of paths in the second step.

Num paths of the first step = 1/3
Num of paths in the second step = 1/6
Answer: 1/18

But intuitively, I took the number of paths that the ant could take to get to D divided by the total number of paths.

Num of paths to d = 1
Num of total paths = 12
Answer: 1/12

Why aren't these paths equivalent? Intuitively They seem the same

#Combinatorics

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Interesting thought, but I think the difference is that in your second approach not all the paths have the same probability of being taken. For example, the path ABC has a probability of 1/3 x 1/3 = 1/9 of being taken, while the path AGC has a probability of 1/3 x 1/6 = 1/18 of being taken. So while you are correct that there are a total of 12 two-step paths, since they don't all have the same odds of being taken we can't simply divide 1 by 12 to get the odds of reaching D in two steps.

Note that the probability of ending at point A is 1/9 + 1/9 + 1/18 = 5/18, at points C and E are each 1/9 + 1/18 = 1/6, at point G is 1/9 + 1/9 = 2/9, while the probability for points B, D, and F are each 1/18. These probabilities add to 5/18 + 2 x 1/6 + 2/9 + 3 x 1/18 = 1 as expected.

Brian Charlesworth - 2 years, 1 month ago

Wow, great explanation thank you!!!

Fernando Hidalgo - 2 years, 1 month ago

You're welcome! :)

Brian Charlesworth - 2 years, 1 month ago

Because the probability of the ant landing on a certain point is not equal for all points, as the second "solution" assumes. For example, If we want the ant to go from A to D in exactly two steps, then it must go through the path A -> G -> D, whereas if we want it to land on C, for example, it could take the A -> G -> C path or the A -> B > C path. And even then, the probability of AGC being taken (1/31/6 = 1/18) is different than the probability of ABC (1/31/2 = 1/6), so the reason why the second solution is wrong is because we can't assume that every point is equally likely to be the one on which the ant will land in the second step.

Rafael Resener - 2 years, 1 month ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$