Atmospheric physics 3: Hydrostatic equation

In fact, the atmosphere consists of compressible gases, so that the mass density $\rho(z)$ of the air decreases continuously with the altitude $z$. However, the weight of the gas layers must be supported by the pressure gradient $\frac{dP}{dz}$ in the atmosphere. The balance of compressive forces and gravitation is expressed by the hydrostatic equation: $\frac{dP(z)}{dz} = -\rho(z) g$ with the gravitational acceleration $g \approx 9.81 \,\text{m}/\text{s}^2$.

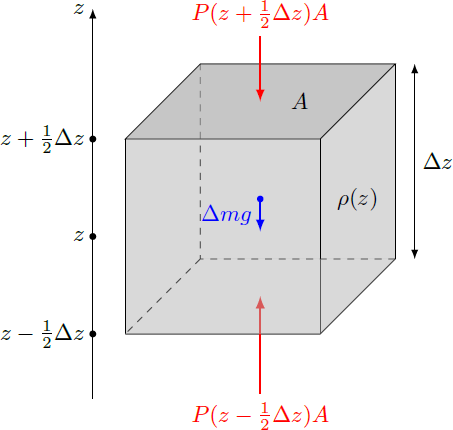
This equation can be derived as follows: We consider a cuboid volume element of the atmosphere with the base area $A$ parallel to the Earth's surface and the height $\Delta z$ (see the diagramm on the right). The mass of this volume is $\Delta m \approx \rho(z) A \Delta z$, so that a weight $\Delta F_g = -\Delta m g$ acts on the entire volume. In addition, the pressures $P(z + \frac{1}{2} \Delta z)$ and $P(z - \frac{1}{2}\Delta z)$ act respectively on the top and bottom of the cuboid. In the static case, the sum of all forces on the volume element must be zero. In the limit $\Delta z \to 0$, the pressure difference changes into the derivative $\frac{dP}{dz}$, so that the difference equation becomes a differential equation. $\begin{aligned} \sum F = 0 &= - \Delta m g - P(z + \tfrac{1}{2} \Delta z)A + P(z + \tfrac{1}{2} \Delta z)A \\ &= -\left(\rho(z) g - \frac{P(z + \tfrac{1}{2} \Delta z)- P(z + \tfrac{1}{2} \Delta z)}{\Delta z} \right) A \Delta z \\ &\stackrel{\Delta z \to 0}{\to} -\left(\rho(z) g - \frac{d P(z)}{dz} \right) dV \end{aligned}$ Since the expression in parentheses must be zero it follows $\boxed{\dfrac{d P(z)}{dz} = - \rho(z) g }$