A baffling geometry question

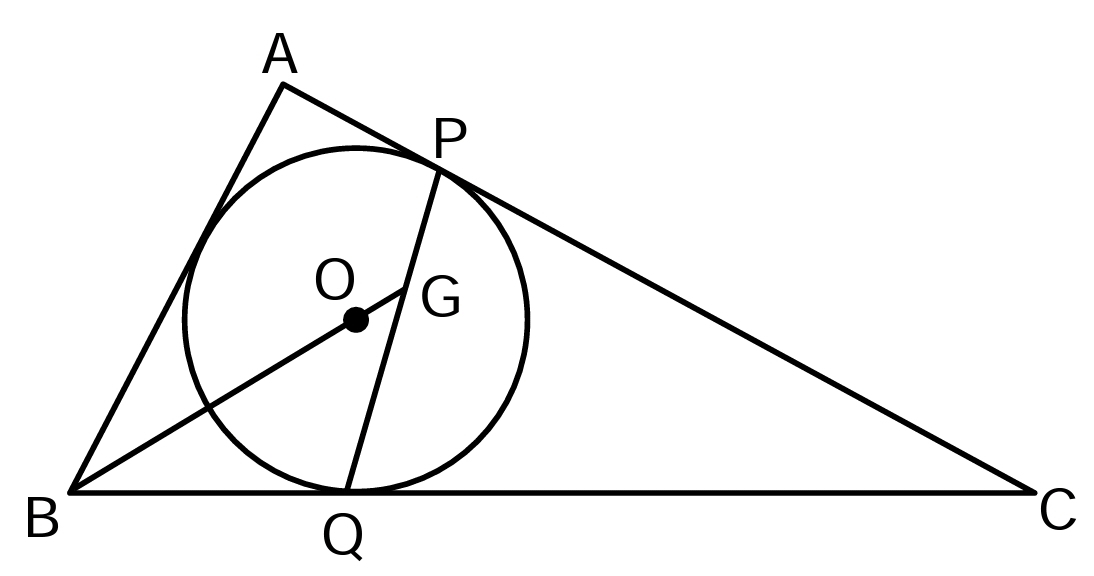
In the given figure, P and Q are point of contact. O is the incentre. Line BO produced, meets PQ at G. Find the value of angle AGB?

The reason i shared the question as a note is that i don't know the answer. Try it out, & if you solve, please post a rigorous solution rather than mere guess.

#Geometry #Trigonometry #TriangleProperties #Triangle #Incircle

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Check out this graphic

Baffling Geometry

With lots of angle-chasing, it can be worked out that, given angles $a, b$ , the following angles are

$\angle OAP=90-a-b$
$\angle OGP=90+a+b$
$\angle AOG=90-a$
$\angle APG=90+a$

Hence, $APGO$ is a cyclic quadrilateral. Moreover, since $APO$ is a right triangle, $AO$ is the diameter of the circle that circumscribes the cyclic quadrilateral $APGO$ . Hence, $AGO$ is also a right triangle, and we have our answer.

Michael Mendrin - 6 years, 9 months ago

Here is another way to prove it. It is easy to see $\angle PQC = {\angle BAC} /2 + {\angle ABC}/2$ . So you can get $\angle BGQ = {\angle BAC} /2 = \angle BAO$ , therefore $\triangle BGQ \sim \triangle BAO$ and $BG \times BO = BQ \times BA$ . Let the point of contact of incircle with AB is D, we have $BG \times BO = BD \times BA$ . So AGOD is cyclic. $\angle AGB = \angle BDO = 90 ^ \circ$

Roger Lu - 6 years, 9 months ago

You haven't defined the point $D$ in this proof. But it is simply the point touching the circle on the segment $AB$ .

mathh mathh - 6 years, 9 months ago

AP PG GB

Shanzkie Vargas - 6 years, 9 months ago

Construct a model diagram with AC and BC AB as tangents

führer sy - 6 years, 8 months ago

With any dimensions of radius and lengths of triangle

führer sy - 6 years, 8 months ago

I took an equilateral triangle and using coordinate geometry found out the value of the angle. Is the method legitimate?

Kartik Raj - 6 years, 9 months ago

You've only found it when the triangle is equilateral. You haven't proved that the angle is the same for all triangles. You can't assume that all the triangles have the same angle just because the question asks for a single unique numeric value.

mathh mathh - 6 years, 9 months ago

führer sy - 6 years, 8 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$