A Big Doubt (Own Theorem)

A few years ago I discovered this property and it supposed to be my own Geometry Theorem. I want to know if is it real. Have you seen a Theorem like this?

As a corollary we can say:

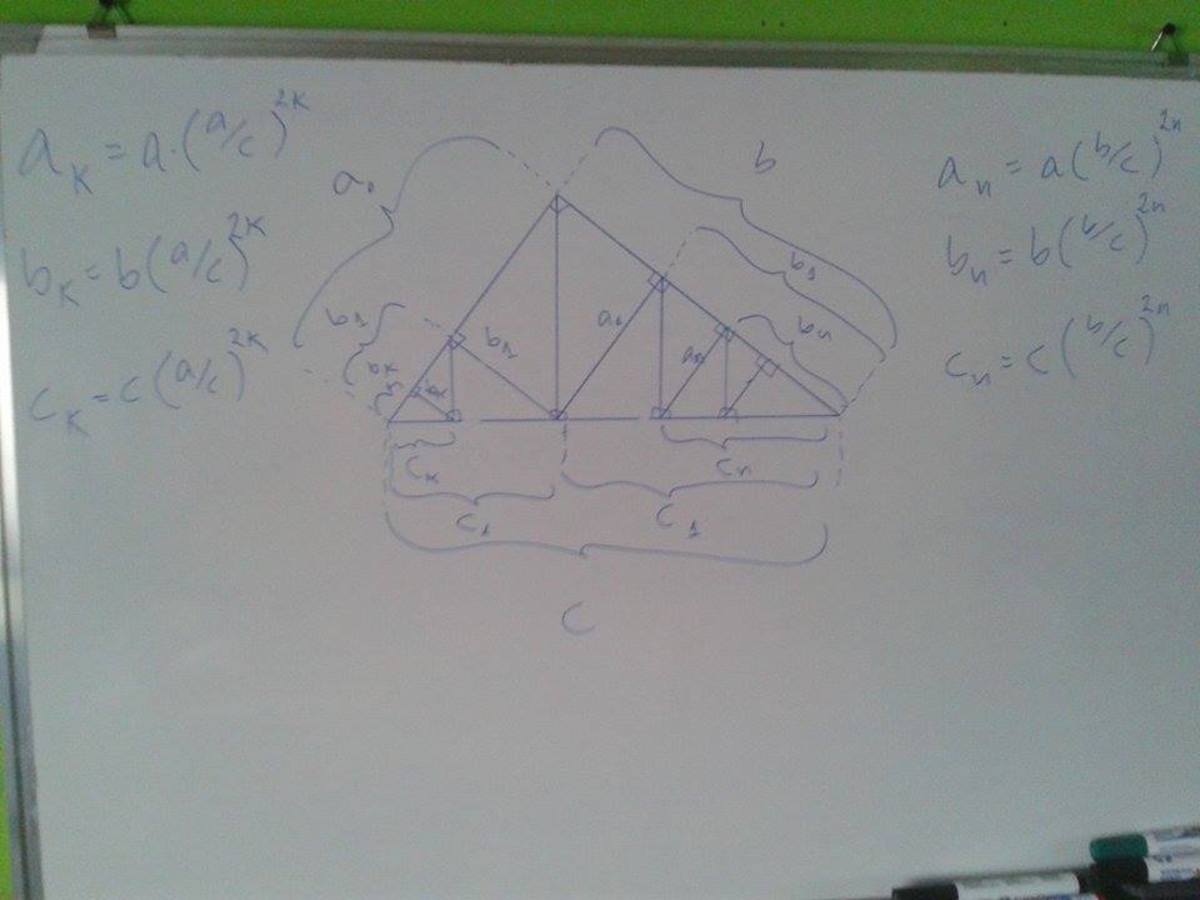
If we let $a$ and $b$ be the foots of a right triangle with hypotenuse $c$ , we have

$\dfrac {c^{2}}{a^{2}} = \sum_{n=0}^\infty (\dfrac{b}{c})^{2n}$ And $\dfrac{c^{2}}{b^{2}}=\sum_{n=0}^\infty (\dfrac{a}{c})^{2n}$

#Geometry #HjalmarPhillippe #OwnTheorem?

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

You would need to explain the set up with some words, in order to explicitly convey what you intend.

Calvin Lin Staff - 5 years, 10 months ago

For the triangle in the above photo we know by euclidean theorem that $a^{2}=pc$ , and $h=\frac{ab}{c}$ . So it is true that - $a_{1} = \frac{c_{1}h}{b}$ - $a_{1}=\frac{\frac{b^{2}}{c}\frac{ab}{c}}{b}=a(\frac{b}{c})^{2}$ It's easy to see that $c_{1}=c(\frac{b}{c})^{2}$ by euclidean theorem. And the same with $b_{1}$ to get $b_{1}=b(\frac{b}{c})^{2}$ . If you take it with the next triangles at that side you'll find that $a_{n}=a(\frac{b}{c})^{2n}$ , $b_{n}=b(\frac{b}{c})^{2n}$ and $c_{n}=c(\frac{b}{c})^{2n}$ And with the triangles at the other side you'll find that $a_{k}=a(\frac{a}{c})^{2k}$ , $b_{k}=b(\frac{a}{c})^{2k}$ and $c_{k}=c(\frac{a}{c})^{2k}$

Hjalmar Orellana Soto - 5 years, 10 months ago

My calculations in Maple show me that it's true for triangles :

(a=4, b = 8.01, c = 8.95)

(a=3, b = 4, c = 5)

(a=4.9875077, b=12.429690, c=13.392999)

John Doe - 5 years, 10 months ago

The corollary or the theorem?

Hjalmar Orellana Soto - 5 years, 10 months ago

I think it's theorem, I have not seen it before.

John Doe - 5 years, 10 months ago

I've seen to problem of this sort. The closed form of $a_{k}$ wasn't given, but we had to sum a very similar series.

A Former Brilliant Member - 5 years, 3 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$