A Complex Thought!

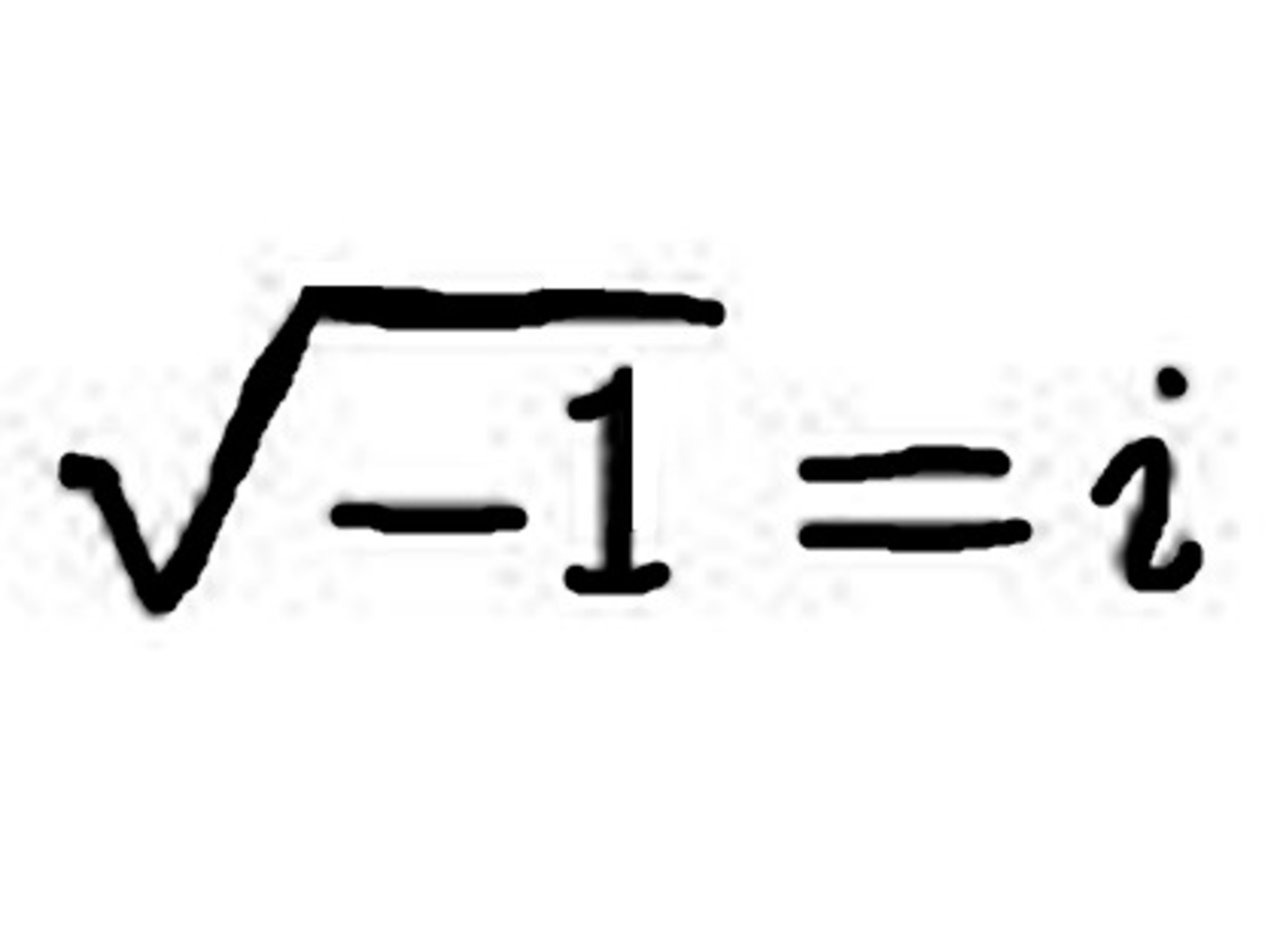
I was just playing around with complex numbers and I came up with something that I found really intriguing, but very bizarre and puzzling.

Note: I am just having fun, so, please do not take the following very seriously..But sure, please tell me in the comments whether it is correct or not.

My first goal was to find the value of $\displaystyle i^i$ . I tackled this in the following way:

Let,
$x = i^i$

Now,
$i = e^{i\frac{\pi}{2}}$

Substituting this value of $\displaystyle i$ ,

$x = \left(e^{i\frac{\pi}{2}}\right)^i$

$\Rightarrow x = e^{i^2\frac{\pi}{2}}$

$x = e^{-\frac{\pi}{2}}$

$\Rightarrow \boxed{i^i = 0.2078}$

After having found this value, I took it one step further (towards insanity!)

What is the value of $\displaystyle i^{i^{i\ldots 'x' times}}$ , where there are $'x'$ iotas.

Let $\displaystyle f(x) = i^{i^{i\ldots 'x' times}}$

Then,
$f(x) = i^{f(x-1)}$

Taking $\ln$ on both sides,
$\ln f(x) = f(x-1)\cdot \ln i$

Note: I know $\ln i$ doesn't exist, but as I said : just having fun.

Differentiate on both sides wrt $x$ ,
$\frac{1}{f(x)}f'(x) = f'(x-1) \ln i$

Assuming $\displaystyle f(x)$ is differentiable over all $x$ ,
Take $\displaystyle\lim_{x\to\infty}$ on both sides.

$\frac{1}{\lim_{x\to\infty}f(x)}\lim_{x\to\infty}f'(x) = \lim_{x\to\infty}f'(x-1)\ln i$

If $\displaystyle\lim_{x\to\infty}f'(x) = L$ , then $\displaystyle\lim_{x\to\infty}f'(x-1) = L$

Thus,
$\frac{1}{\lim_{x\to\infty}f(x)} = \ln i$

$\Rightarrow \lim_{x\to\infty}f(x) = \frac{1}{\ln i}$

Therefore,

$i^{i^{i\ldots}} = \frac{1}{\ln i} = \frac{2}{i\pi}$

I know this may be terribly wrong, but I was just bored of studying, and decided to do all this crazy stuff just for fun.

Anyways, please be nice in the comments and tell me what you think.!

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Discovered the following later on :

In the process, we did the following,

$f(x) = i^{f(x-1)}$

$\ln f(x) = f(x-1)\ln i$

Take $\displaystyle\lim_{x\to\infty}$ on both sides,

$\ln\left(\lim_{x\to\infty}f(x)\right) = \ln i \times\lim_{x\to\infty}f(x-1)$

We found out in the end that,

$\lim_{x\to\infty}f(x) = \lim_{x\to\infty}f(x-1) = \frac{1}{\ln i}$

Substituting this value,

$\ln\left(\frac{1}{\ln i}\right) = \ln i \times\left(\frac{1}{\ln i}\right)$

$-\ln\left(\ln i\right) = 1$

$\boxed{\ln\left(\ln i\right) = -1}$

Now, Im sure I am crazy!

Anish Puthuraya - 7 years, 2 months ago

Well magnitude of 1/logi isn't 1 but i^i^i.... should have magnitude 1 right

Milun Moghe - 7 years, 2 months ago

But i^i^i should be (e-^minus pi/2)^i which is -i. Magnitude is 1, if you take modulus.

Rohan Rao - 7 years, 2 months ago

@Rohan Rao – But magnitude of I/logi isn't 1

@Milun Moghe – Yes, ur right.

But searching google for ln(ln(I)) gives 0.451582705 + 1.57079633 i And so does Wolfram Alpha...

Yes, indeed. There must be some flaw in my crazy proof. I dont know.

Not offencive but I think that assuming the limit exists is wrong

Maybe. I wasn't offended. I expected corrections..This was purely for fun.

@Anish Puthuraya – I think that when you differentiated the function caused the anomaly. $f(x)$ is not exactly a function in x i.e., as a variable. It is rather somewhat a parameter which denotes the number of iotas. Though the value of $\f(x)$ depends upon x, it is ultimately a constant. Moreover, x can assume only distinct values, the natural numbers. Therefore, is not continuous in that sense.

To put my view in a better way, $f(x)$ is somewhat like floor function. It accepts different values of x and returns some constant values. Also the floor function is derivable only in specific domains and always returns zero as the value of the function in a way independent of x.

Similarly here, I'm quite certain that when you cancelled the limits, you made the error there by cancelling zero on either side of the equation.

Try it without differentiating, then mostly the anomaly will not rise.

Sudeep Salgia - 7 years, 2 months ago

@Sudeep Salgia – Awesome man! Nice observation. That makes sense! From this, I just remembered a paradox related to the above:

Consider $f(x) = x^2$ . Differentiating, we get $f'(x) = 2x$ . Now, $f(x)$ can be written as $x+x+x+\ldots+\text{ x times }$ . Differentiating term-wise, we have $1 + 1 + 1 + \ldots + \text{ x times } = x$ .

The problem is, in writing $f(x) = x+x+x+\ldots+\text{ x times}$ , we assume $x$ to be an integer!

Similar to what's going on here.

Parth Thakkar - 7 years, 2 months ago

@Parth Thakkar – Thank you both of you.!

It may be a bit surprising that $i^i$ has an infinite number of real values. Recall that $e^{i\theta}=e^{i(\theta+2\pi n)}$ for any integer $n$ . Thus, we have that $i^i=(e^{i\frac{\pi}{2}+2i\pi n})^i=e^{-\frac{\pi}{2}+2\pi n}$ for any integer $n$ .

Daniel Liu - 6 years, 11 months ago

The problem with complex numbers. They don't exist. :D

Sharky Kesa - 6 years, 11 months ago

AWESOME! That's kind of how my brain works, go off on some crazy tangent, and usually create a problem. :D

Finn Hulse - 7 years, 1 month ago

Great minds think alike. :D

it's close, but the Lambert W function is defined as satisfying the equation

$z=W(z){ e }^{ W(z) }$

so that in solving the equation for this infinite tower function

$z={ i }^{ z }$

it works out that

$z=(W(\frac { \pi }{ 2i } ))(\frac { 2i }{ \pi } )$

and that first term isn't quite $1$ , but is some complex number. This problem was already answered in the mid 1800s.

Michael Mendrin - 6 years, 11 months ago

x was originally defined as an integer. How come x is differentiable over x

Debasish Ray Chawdhuri - 7 years, 2 months ago

You can't differentiate the function because it is discrete: x must be a positive integer.

Kenny Lau - 6 years, 11 months ago

i think gud work out really gud for you

Kushank Bansal - 6 years, 4 months ago

Which is (-2i/pi)

In breaking rules we discover newer better rules. This was fun. I have for too long been a non serious mathematician to come in meaningfully but I can tell you that I loved this post.

Such craziness was in fact the default way we used to prep for IIT JEE. And that was in a different era when coaching was optional ( and it was a suboptimal approach too if you chose not to take it!)

Anyways long story short , Dirac did mathematical craziness like this that led to the concept of antimatter.

And your jottings here reminded me of pretty similar jottings lying somewhere in my old notebooks!

Also a fellow fanboy of Euler and specifically of Euler's formula! :)

arka bhattacharya - 5 years, 9 months ago

can you tell me i^i^i^i^.................infinity = ? if every one is having fun, why not i?

A Former Brilliant Member - 4 years, 10 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$