A game of dice

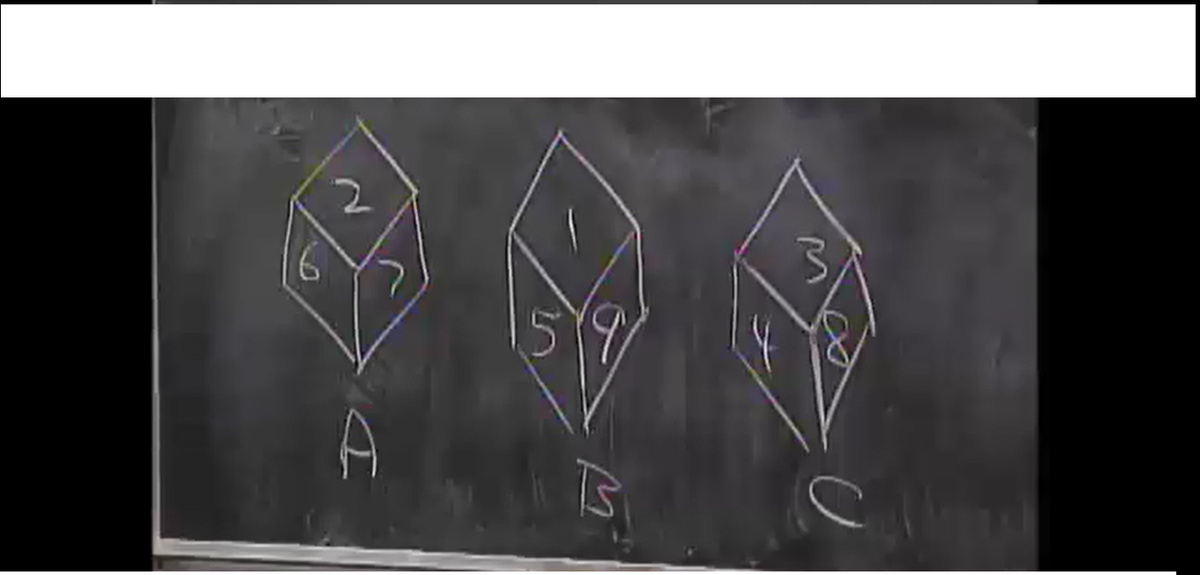
You are given 3 dice as shown in the figure above where the numbers on the opposite faces of the each of the dice are equal.(For example,the number opposite to 6 in the first dice is also 6.)

Now the game begins like this I choose 1 dice and you choose another one from the remaining and after rolling whichever comes up with larger value wins the game.By choosing which dice are you more likely to win(that is with greater probability) in the following cases:

A.I choose dice A.

B.I choose dice B

C.I choose dice C

#Combinatorics #Probability #Goldbach'sConjurersGroup #TorqueGroup #IntroduceYourself

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

A beats B, B beats C, and C beats A, all with 5/9 probability. Nontransistive dice, i.e, A > B > C > A

Michael Mendrin - 7 years ago

Haha....indeed....but rolling twice the case becomes entirely opposite.....but does a pattern hold if we generalize it to k rolls?

Eddie The Head - 7 years ago

I believe non-transitive dice were discovered, if not just made popular, by Dr. James Grime (seen on numberphile)?

Daniel Liu - 7 years ago

Yeah...I remember seeing that on numberphile too....

Eddie The Head - 7 years ago

A. I will choose dice C B. I will choose dice A C. I will choose dice B

Venkii Rv - 7 years ago

Though withoutvan answer its a beautiful question

Muhsin Haneefa - 7 years ago

If you want the answer you may choose to read on non-transitive dice

Eddie The Head - 7 years ago

A is actually no better than B, and B is no better than C. If u calculate the expected values, they are just the same. This means it will be a fair bet between any chosen pair of dice if u include the rewards for winning a bet as the difference in numbers rolled on the dice. When we choose A to bet with B, for instance, it is possible to get more rewards on B (example: u roll a 9) even when there is a lower probability (4/9) to win.

Cheah Chung Yin - 7 years ago

I choose c...c<a

Shrevarna Shaji - 7 years ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$