A limit problem

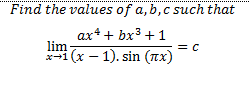
I have a problem in limit that made me curious until now. The problem is about the limit and trigonometry. I don't know how to simplify it.. pls help me to solve it. thanks..:)

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I assume $c$ is a finite value

The key here is L'hôpital's Rule (3 times)

Substitution of $x=1$ must give an indeterminate form of $\frac {0}{0}$ because denominator yields $0$

So the numerator is equals to $0$ when $x=1 \Rightarrow a+b+1=0$

Apply L'hôpital's Rule and chain rule, the limit becomes

$\frac {4 a x^{3} + 3 b x^{2}} { \pi (x - 1) \cos (\pi x) + \sin (\pi x) }$

And it must yield an indeterminate form of $\frac {0}{0}$ as well because denominator yields $0$ at $x=1$ , thus numerator must yield $0$ as well

So, $4a+3b=0$ , solve the two equations gives $a = 3$ , $b=-4$

Now substitute those two values into the limit and apply L'hôpital's Rule Rule once again

$\frac {36 x^{2} - 24 x } { \pi [ -(x-1) \pi \sin (\pi x) + \cos (\pi x) ] + \pi \cos (\pi x) }$

Substitute $x=1$ gives $c = - \frac {6}{\pi}$

Hence, $a = 3, b=-4, c = - \frac {6}{\pi}$

By the way, I'm new to LaTeX, anyone know how to increase size of the mathematical symbols used? The fractions displayed are too small in standard font size.

Pi Han Goh - 8 years ago

yeah agreed......with the answer...:)

A Former Brilliant Member - 8 years ago

thanks for the answer, Pi Han..I never consider the using of 0/0 to evaluate the value of numerator, then apply L'hopital more than twice to find the answer. Anyway, thanks for the great answer..I need to learn more again about the L'Hopital rule. :)

Leonardo Chandra - 8 years ago

from where did u get this problem?

Vamsi Krishna Appili - 8 years ago

I got this problem from my calculus book. this problem is about limit problems..an introduction to improper form of limit..:)

Leonardo Chandra - 8 years ago

How about We asume that limit when $x \rightarrow 1$ is 0/0. Then, calculate it using L'Hopital Theorem.. Sorry, I haven't tried that before..

Andrias Meisyal - 8 years ago

since denominator at x=1 tends to 0 then for the limit to exist ,numerator has to be 0 or else it will form indeterminate form....

0/0 is a basic form in limits....:)

A Former Brilliant Member - 8 years ago

thank you very much for explanation :)

Andrias Meisyal - 8 years ago

@Andrias Meisyal – no problem....

A Former Brilliant Member - 8 years ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$