A line and area of a triangle

Here's a statement Area of triangle formed by the line passing through the point $\left( \alpha ,\beta \right)$ , with axes is maximum when point $\left( \alpha ,\beta \right)$ is the midpoint of the line between the axes.

The question was to answer whether the statement was correct or not and the answer given is that the statement is WRONG.

But why?

Here's what I did,

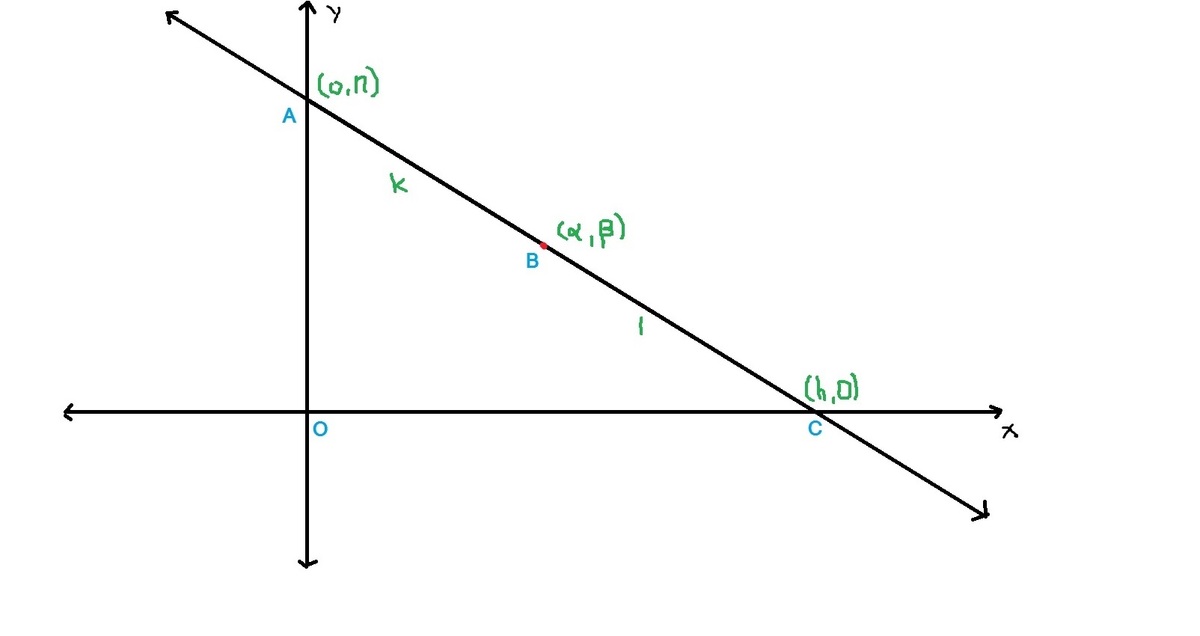
Let $A(0,n)$ , $B(\alpha,\beta)$ , $C(h,0)$ and $AB:BC::k:1$

We know, $\alpha =\frac { kh }{ k+1 } \quad \& \quad \beta =\frac { n }{ k+1 }$

$\Rightarrow h=\frac { \alpha \left( k+1 \right) }{ k } \quad \& \quad n=\beta \left( k+1 \right)$

Area of $\Delta AOC$ , $A=\frac { 1 }{ 2 } \times \frac { \alpha \left( k+1 \right) }{ k } \times \beta \left( k+1 \right)$

Differentiating w.r.t k,

$\Rightarrow \frac { dA }{ dk } =\frac { 1 }{ 2 } \alpha \beta \left[ \frac { 2k\left( k+1 \right) -{ \left( k+1 \right) }^{ 2 } }{ { k }^{ 2 } } \right]$

Equating $\frac { dA }{ dk }$ to zero $\Rightarrow k=\pm 1$

Maxima occurs at $k=1$

$\therefore$ Area is maximum when $k=1$ .

$k=1\Rightarrow$ $(\alpha,\beta)$ is the midpoint of $A$ and $C$ .

Hence, Statement is CORRECT.

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

An application of AM-GM will tell you why you've gotten the wrong answer.

Note that $\dfrac{x}{a} + \dfrac{y}{b} = 1$ is the equation of the line in intercept form. $a$ and $b$ are the $x$ and $y$ intercepts respectively.
We need to maximize $\triangle = \dfrac{ab}{2}$ .
As $\alpha, \beta$ lies on the line, $\dfrac{\alpha}{a} + \dfrac{\beta}{b} = 1 \geq 2 \sqrt{\dfrac{\alpha \beta}{2 \triangle}}$
$\Rightarrow \triangle \geq 2 \alpha \beta$ with equality when $\dfrac{\alpha}{a} = \dfrac{\beta}{b} = \dfrac{1}{2}$

So you have the minimum area, not the maximum.
Be careful when using calculus to find extrema - check minima and maxima always.

Ameya Daigavane - 5 years, 2 months ago

Oh! yes sir, I made a mistake while checking maxima and minima! And your approach is superb!

The red curve represent $\frac { dA }{ dk }$ and green curve represent $\frac { { d }^{ 2 }A }{ d{ k }^{ 2 } }$

Anandhu Raj - 5 years, 2 months ago

@Ameya Daigavane Sorry disturb you again, sir. But could you please post a solution to below question?

A variable line, drawn through the point of intersection of the straight lines $\frac { x }{ a } +\frac { y }{ b } =1$ and $\frac { x }{ b } +\frac { y }{ a } =1$ , meets the coordinate axes in $A$ and $B$ . Then find the locus of the midpoint of $AB$ .

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$