A math problem is able to have multiple right solutions
This "riddle" has raised more than one million comments on Facebook.
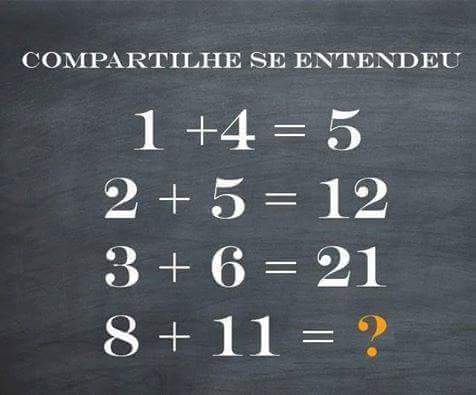
What would be your answer to the question mark? The most common answers are 40 and 96... Does anyone could say why? Hence if it is given the first terms in a sequence and the sequence is not well defined, the next term is able has multiple right solutions, even infinite solutions. For instance, in the next problem Find the solution which I gave one solution, is able to have infinite answers, even the other answers given in the problem can be right... Just only have to take polynomials with two variables x,y which satisfies the conditions, for example,can you find a polynomial with variables x, y satisfying the first conditions and such that f(13,4) = 123 or f(10,9) = 123?... So my conclusion is this one: Can you post one riddle where different right solutions are valid?and why my "riddle" is able to have 40 or 96 as valid solutions?can you find other right solution and say why?
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
I think they expect 96 as the answer if they do this. a+b=a×(b+1) But like @Nihar Mahajan said you can have ∞ solutions
The riddle has infinitely many solutions using LZOB or Lagrange interpolation, since the choices are not provided.
Log in to reply
Why are you assuming the function is a polynomial? (just asking)
Log in to reply
Its not wrong to assume a polynomial right?
Log in to reply
I could be any arbitrary function of two variables for that matter as we've not been given that the function IS a polynomial.
Log in to reply
So it can be ∞ if its a polynomial and if its some other function it can have finite or infinite. Therefore in general it can be said infinite
Log in to reply
please, be calm. I can not answer to everybody....
Log in to reply
Hey I was asking @Deeparaj Bhat. And it was a comment and not a question
Log in to reply
ok, sorry, my apologies
please, be calm. I can not answer to everybody
How is the answer 96 or 40?
Log in to reply
I got 96 but not 40.
Log in to reply
ok, 96 can be got of this form, ⎩⎪⎨⎪⎧1+4=1⋅4+1=52+5=2⋅5+2=123+6=3⋅6+3=21 so I can say 8+11=8⋅11+8=96. Now, we are going to get 40,ok...please, be cal, wait my answer,haha..
Log in to reply
Wait, I will wait. (LOL)
Log in to reply
Now, we are going 40.. We can consider (1,4), (2,5), (3,6) and (8,11) to be the first terms of one sequence in N2 and 1+4=5 and we can define for the next terms its sum added to the sum obtained before. Hence 2+5=7+ sum obtained before =7+5=12 , now 3+6=9+ sum obtained before =9+12=21 so 8+11=19+ sum obtained before =19+21=40
Log in to reply
Oh! I considered 8,11 as the eighth term!
Log in to reply
but, they can be considered the first terms in a sequence. Now I'm going with the Lagrange interpolation
please, be calm. I can not answer to everybody
please, be calm. I can not answer to everybody
Log in to reply
We have f(5,3)=28, f(12,10)=222 ,f(9,1)=810, f(4,2)=26, f(8,3)=511,f(10,1)=911, f(7,3)=410. This problem using Lagrange interpolation is able to have ∞ answers. For example, I want furthemore f(13,9)=123. Is evrything allright so far? haha. Ok, I'm going to look for a polynomial with variables x,y and some constants a,b,c,d,e,f,g,h,i, ...fullfiling these conditions,(notice I'm going to repeat this factor (y -1) and (y - 3), I would not to do it, but I'm going to do it for clarity) so the polynomial has to be f(x,y)=a(x−5)(y−3)(x−12)(y−10)(x−9)(y−1)(x−4)(y−2)(x−8)(y−3)(x−10)(y−1)(x−7)(y−3)+ +b(x−5)(y−3)(x−12)(y−10)(x−9)(y−1)(x−4)(y−2)(x−8)(y−3)(x−10)(y−1)(x−13)(y−9)+ +c(x−5)(y−3)(x−12)(y−10)(x−9)(y−1)(x−4)(y−2)(x−8)(y−3)(x−7)(y−3)(x−13)(y−9)+ +d(x−5)(y−3)(x−12)(y−10)(x−9)(y−1)(x−4)(y−2)(x−10)(y−1)(x−7)(y−3)(x−13)(y−9)+... and get the constants a,b ,c ,d e,f, g, h,... fulfilling the requisites... so this problem has ∞ right solutions... Ok, now I'm going to eat... Later I'll review the comments
Exactly, for the problem Find the solution you can use Lagrange interpolation with two variables, please wait a bit, and I'll give the answer
52
Assuming there is something fundamental operation that isn't explicit, just like the assumption that the last answer is also added to the next equation... Goes like this... The pattern is multiplying the second number secretly by a sequential while number, just like secretly having the last answer added to the next equation...
1+(4[×1])=5 2+(5[×2])=12 3+(6[×3])=21 8+(11[×4])=52
This makes all the answers correct.
Log in to reply
1+(4[×1])=5
2+(5[×2])=12
3+(6[×3])=21
8+(11[×4])=5
The answer is 40. :P
In this riddle the answer of the previous statement is added to the terms of the original statement.
First statement starts with 1 + 4 = 5.
Second statement:- 5 + 2 + 5 = 12.
Third statement:- 12 + 3 + 6 = 21.
Fourth statement should be 21 + 8 + 11 = 40.
Log in to reply
1+(4[×1])=5
2+(5[×2])=12
3+(6[×3])=21
8+(11[×4])=52Log in to reply
That was supposed to be a clarification of my own post... Sorry. 'Doing this from my phone while walking to the store.