What is the Acceleration?

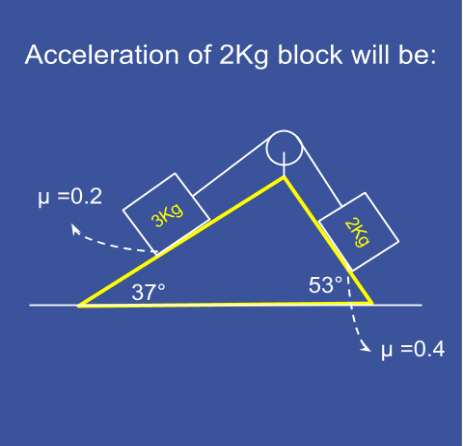
Find the acceleration of the $2\text{ kg}$ block in $\text{ms}^{-2}$ ?

Source: This beautiful question appeared at eagerbug.com . I hope everyone like solving it.! :)

#Mechanics

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Let me revise frictional force topic again has been two years since I last learned it ;)

Ashish Menon - 5 years ago

As you say my friend:-)

Rishabh Tiwari - 5 years ago

If those are static friction coefficients, then $a = 0$ is possible.
If these are kinetic friction coefficients, write the force balance for each block. I'm assuming the wedge is massless.
The centre of mass will move downwards only, so acceleration of the heavier block will be down the plane, and the lighter one will move up the plane. As the string does not extend/contract, these accelerations are same in magnitude.
Can you solve it from here?

Ameya Daigavane - 5 years ago

Right sir, thank you.!

Rishabh Tiwari - 5 years ago

I guess Ameya already answered it. ;)

A Former Brilliant Member - 5 years ago

@A Former Brilliant Member – Does that mean you won't post a solution? Please do! I need to understand it completely!

Rishabh Tiwari - 5 years ago

Taking the 3kg block accelerating downwards $T-\mu mg\cos { \theta } -mg\sin { \theta } =ma\quad \quad \quad \quad \quad \quad \quad \quad \quad \left( 1 \right) \\ Mg\sin { \alpha } -\mu 'Mg\cos { \alpha } =Ma\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left( 2 \right) \\ Adding\quad 1\quad and\quad 2\quad we\quad get\\ \left( M\sin { \alpha } -m\sin { \theta } \right) g-g\left( \mu 'M\cos { \alpha } +\mu m\cos { \theta } \right) =\left( M+m \right) a\\ \Rightarrow 18-16-4.8-4.8=5a\\ \Rightarrow a=-\frac { 7.2.2 }{ 5 } =-1.52m{ s }^{ -2 }\\ \\$ - sign means that the acceleration of the system is in opposite direction to that I have assumed here, i.e. 2kg block slides downward. However taking the other block(i.e. 2kg) accelerating downwards, $-18+16-4.8-4.8=5a\\ \Rightarrow a=-\frac { 11.6 }{ 5 } =-2.32m{ s }^{ -2 }\\$ As these results are contradictory, I think that the system wont accelerate. So a=0

Swagat Panda - 4 years, 12 months ago

Please retry and calculate and see if your answer matches with the options I have provided.

Rishabh Tiwari - 4 years, 12 months ago

@Swapnil Das ; a good problem for you & for the physics section, I hope ! :-)

Rishabh Tiwari - 5 years ago

@Ashish Siva, @Deeparaj Bhat , @Abhay Tiwari , please comment!

Rishabh Tiwari - 5 years ago

Sorry Rishabh, I am not good at this topic.

Abhay Tiwari - 5 years ago

Not a problem bro, Ur Perfect! Me2 not good at this.

Rishabh Tiwari - 5 years ago

@Rishabh Tiwari – I am not sure but I guess the 3kg will pull with a Force of $F=g[(3 \space Sin (37°)-0.2×3 ×\space Cos(37°))\space - \space (2 \space Sin (53°)-0.4×2× \space Cos(53°))]=2.1481 \space kg \space ms^{-2}$ , if $g=10 \space ms°^{-2}$

Abhay Tiwari - 5 years ago

@Abhay Tiwari – I think the second half of the force is not needed, first half would be the force driving the $3kg$ block down & you also have to subtract tension from that!

Rishabh Tiwari - 5 years ago

@Rishabh Tiwari – Ha ha. Let me see if somebody posts a solution. Maybe then I will understand.

Abhay Tiwari - 5 years ago

@Abhay Tiwari – Ya right, I expect a good solution from @Swapnil Das or @Deeparaj Bhat , however, anyone is free to post a solution! :-)

Rishabh Tiwari - 5 years ago

Hey does anyone know the answer? I got $\boxed{1.52 m/s^2}$

abc xyz - 4 years, 12 months ago

Also according to my solution the 2 kg block moves up the slope @Rishabh Tiwari Do you know the correct answer ?

abc xyz - 4 years, 12 months ago

I don't know the answer but here are the options:

(a) 2 (b) 0

Rishabh Tiwari - 4 years, 12 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$